普通最小二乘法 (Ordinary Least Square,简称 OLS) 是回归方法中最简单,应用最多的一种方法。OLS 可为用户想要了解/预测的变量或过程提供全局模型;还可创建表示该过程的单回归方程。地理加权回归 (GWR) 是若干空间回归方法中的一种,被越来越多地用于地理及其他学科。通过对数据集中的各要素拟合回归方程,GWR 可为用户想要了解/预测的变量或过程提供了一个局部模型。
功能入口
- 空间统计分析 选项卡 -> 空间关系建模 -> 普通最小二乘法 。(iDesktopX)
- 工具箱 -> 空间统计分析 -> 空间关系建模 -> 普通最小二乘法 。(iDesktopX)
主要参数
- 源数据 :设置待分析的矢量数据集,支持点、线、面三种类型的数据集。注意:源数据集中的对象个数要大于 3。
- 解释变量 :解释变量是自变量,即回归方程右侧的 X,可勾选一个或多个数值型字段作为解释变量,用于对因变量的值进行建模或预测。 注意 :若某解释变量的值都相等,则 OLS 的回归方程无法求解。
- 建模字段 :即因变量,待研究或预测的变量,位于回归方程的左侧,只支持数值字段。需根据已知的观测值来构建回归模型,进而得到预测的因变量。
- 结果数据 :设置结果数据所要保存在的数据源及数据集名称,与源数据的数据类型一致。
结果输出
普通最小二乘法的分析结果中的预测值、残差和标准化残差会记录在结果数据集的属性字段中,而 OLS 模型的分布统计量、统计量概率、AICc 和判定系数等统计结果,将显示在OLS报表中。分析结果说明如下:
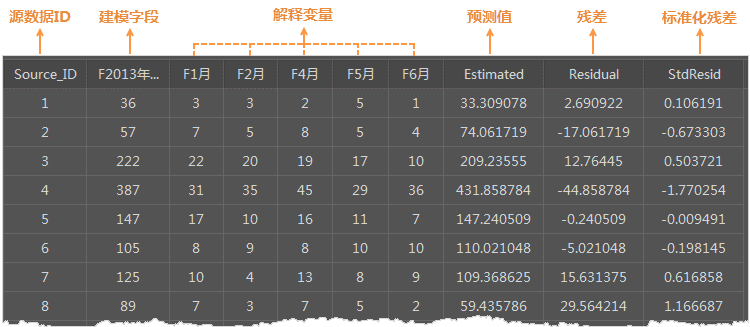
属性表中的结果
- Source_ID :源数据集中对象的 SmID 值,即对象的唯一标识。
- 建模字段与解释字段 :保留了源数据中的建模字段和解释字段。
- Estimated(预测值) :根据指定的解释变量,通过OLS分析得到的拟合值。
- Residual(残差) :这些是因变量无法解释的部分,是估计值和实际值之差,标准化残差的平均值为0,标准差为1。残差可用于确定模型的拟合程度,残差较小表明模型拟合效果较好,可以解释大部分预测值,说明这个回归方程是有效的。可对残差进行空间自相关分析,若高残差或低残差的统计显著性聚集,则表明模型中的某个关键变量缺失了。此时 OLS 结果不可信。
- StdResid残差 :标准残差即残差和标准误差的比值,该值可用来判断数据是否异常。如果标准残差呈现正态分布,则表示此模型的表现比较优异;若出现了严重的偏态,则表示模型有偏差,可能该模型的某个关键变量缺失。若数据都在(-2,2)区间内,表明数据具有正态性和方差齐性;若数据超出(-2,2)区间,表明该数据为异常数据,无方差齐性和正态性。
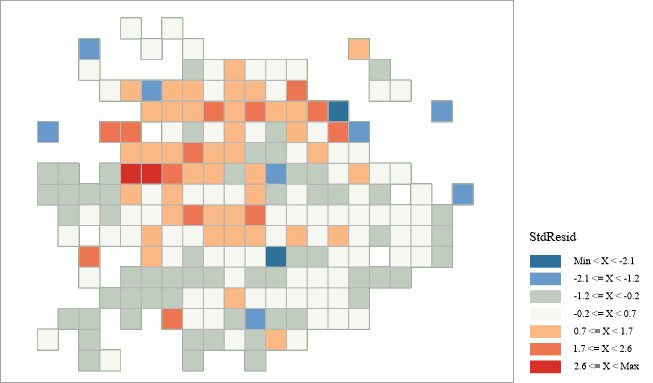
模型残差可视化
执行结束后,将在地图窗口生成模型残差分段专题图。正确的回归模型的偏高预测值或偏低预测值是随机分布的,若偏高预测值或偏低预测值呈聚类分布,则表示至少丢失了关键解释变量。检查模型残差的分布情况,从残差分布特征了解这些聚类区域可能丢失哪些解释变量。有时,对模型残差执行 热点分析 可帮助您确定残差的分布情况。
OLS报表
执行结束后,将在输出窗口生成OLS报表,报告中详细地记录了OLS分析结果,包括模型变量情况、模型显著性分析、变量分布与关系、标准化残差直方图和残差与预测值散点图。具体如下:
-
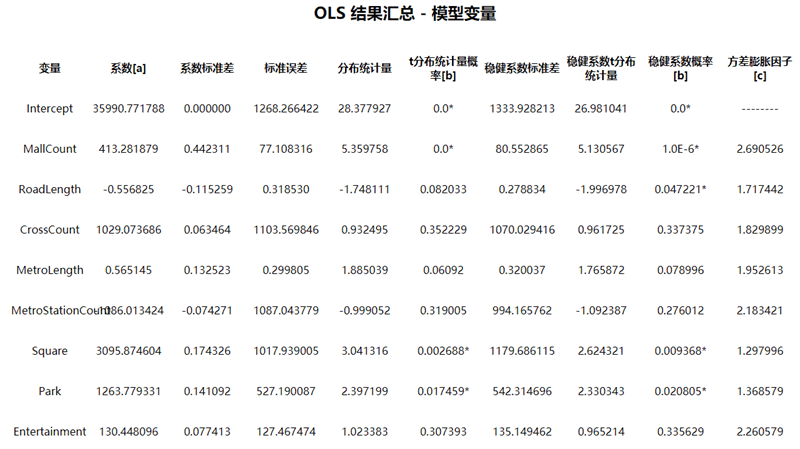
模型变量
- 系数 :系数反映了每个解释变量与因变量之间的关系强度和关系类型。系数的绝对值越大,表示该变量在模型里面贡献越大,也表示该解释变量与因变量的关系越紧密。系数反映了所有其他解释变量保持不变时,关联的解释变量的每单位变化导致其因变量发生的预期变化量。例如,保持其他解释变量不变的情况下,人口普查区块每增加1人,入室盗窃系数就会增加 0.005。同时,系数也表示了解释变量与因变量之间的关系类型,系数为正,表示正相关,例如,人口越多,入室盗窃的数量就越多;系数为负,表示负相关,例如,距离城镇中心的距离越大,入室盗窃的数量就越少。
- 系数标准差 :表示不同解释变量的离散程度。
- 标准误差 :这些值用于衡量每个系数估计值的可靠性。标准误差越小,模型估计值的可信度就越高;标准误差较大,可能表示局部多重共线性存在问题。
- 分布统计量 :用来评估某个解释变量是否具有统计显著性,t分布统计量=平均值 / 标准误差。一般来来说,这个值表示,与P-value意义差不多,都是在验证零假设的情况下,模型的显著性,但是有些时候P-value会有一些问题,比如丢失一些信息。计算机里面进行统计验证的时候,t统计量越大,表示越显著。
- 概率 :当概率 p 值很小时,则系数实际为零的几率也会很小。
- 稳健系数标准差 :就是通过修改(增添或者删除)变量值,看所关注解释变量的回归系数和结果是否稳健。
- 稳健系数t分布统计量 :用来评估稳健系数是否具有统计显著性。
- 稳健系数概率 :如果 Koenker(Breusch-Pagan)具有统计显著性,则应使用稳健概率来评估解释变量的统计显著性。
- 方差膨胀因子 :Variance Inflation Factor(VIF),这个值主要验证解释变量里面是否有冗余变量(即是否存在多重共线性)。一般来说,只要方差膨胀因子超过 7.5,就表示该变量有可能是冗余变量。
-
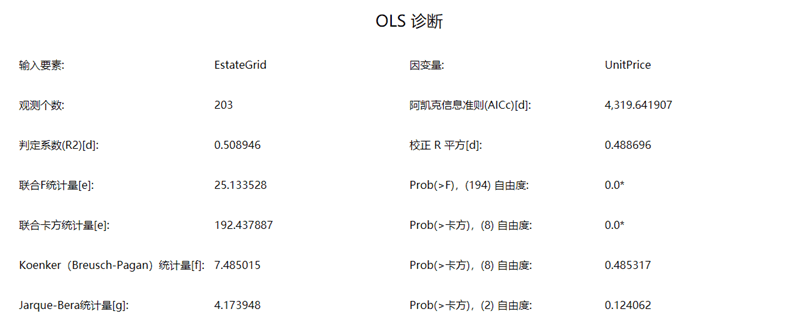
模型显著性
- AIC :是衡量模型拟合优良性的一种标准,可以权衡所估计模型的复杂度和模型拟合数据的优良性,在评价模型时是兼顾了简洁性和精确性。表明增加自由参数的数目提高了拟合的优良性,AIC 鼓励数据的拟合性,但是应尽量避免出现过度拟合的情况。所以优先考虑 AIC 值较小的,是寻找可以最好的解释数据但包含最少自由参数的模型。
- AICc (Akaike):当数据增加时,AICc收敛为AIC,也是模型性能的一种度量,有助与比较不同的回归模型。考虑到模型复杂性,具有较低 AICc 值的模型可更好的拟合观测数据。AICc 不是拟合度的绝对度量,但对于比较用于同一因变量且具有不同解释变量的模型非常有用。如果两个模型的 AICc 值相差大于3,具有较低 AICc 值的模型将视为更佳的模型。
- 判定系数(R 2):判定系数是拟合度的一种度量,其值在0.0和1.0范围内变化,值越大说明模型越好。R2可解释为回归模型所涵盖的因变量方差的比例。R2计算的分母为因变量值的平方和,添加一个解释变量不会更改分母但是会更改分子,这将出现改善模型拟合的情况,但是也可能假象。
-
校正R平方 :校正R平方的计算将按分子和分母的自由度对它们进行正规化。这具有对模型中变量数进行补偿的效果,由于校正的R2值通常小于R2值。但是,执行校正时,无法将该值的解释作为所解释方差的比例。自由度的有效值是带宽的函数,因此,AICc是对模型进行比较的首选方式。
这两个系数的取值,都在0-1之间,可以转换为百分数,通常指的是自变量方程对因变量的解释能力。比如等于0.8的时候,表示回归方程能够解释80%的因变量的变化。这个平方系数越高,那么他们的重合度就越高。而校正 R 平方系数,通常要比多重R平方系数要稍微低一些,因为这个系数的技术与数据的情况关系更强,所以对模型的性能评估也更加准确一些。
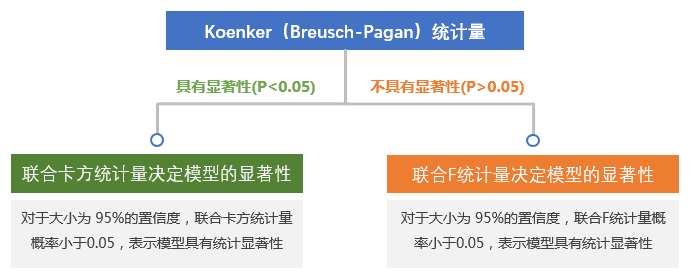
- 联合F统计量 :联合 F 统计量用于检验整个模型的统计显著性。只有在Koenker(Breusch-Pagan)统计量不具有统计显著性时,联合F统计量才可信。检验的零假设为模型中的解释变量不起作用。对于大小为 95%的置信度,联合F统计量概率小于0.05表示模型具有统计显著性。
- 联合F统计量的概率 :用于检验联合 F 统计量是否具有显著性。对于大小为 95%的置信度,联合F统计量概率小于0.05表示模型具有统计显著性。
- 联合F统计量自由度 :自由度与解释变量的个数有关,解释变量的个数越多,自由度就越大。
- 联合卡方统计量 :联合卡方统计量用于检验整个模型的统计显著性。只有在Koenker(Breusch-Pagan)统计量具有统计显著性时,联合F统计量才可信。检验的零假设为模型中的解释变量不起作用。对于大小为95%的置信度,联合F统计量概率小于0.05表示模型具有统计显著性。
- 联合卡方统计量的概率 :用于检验Koenker(Breusch-Pagan)统计量是否具有显著性。对于大小为 95%的置信度,Koenker(Breusch-Pagan)统计量概率小于0.05表示模型具有统计显著性。
- 联合卡方统计量自由度 :自由度与解释变量的个数有关,解释变量的个数越多,自由度就越大。在卡方分布中,自由度越大,那么卡方分布就越接近正态分布。
- Koenker(Breusch-Pagan)统计量 :Koenker 的标准化 Breusch-Pagan 统计量,能评估模型的稳态,用于确定模型的解释变量是否在地理空间和数据空间中都与因变量具有一致的关系。检验的零假设为检验的模型是稳态的。对于大小为95%的置信度,Koenker(Breusch-Pagan)统计量的概率小于0.05表示模型具有统计显著异方差性或非稳态。当检验结果具有显著性时,则需要参考稳健系数标准差和概率来评估每个解释变量的效果。
- Koenker(Breusch-Pagan)统计量的概率 :用于检验Koenker(Breusch-Pagan)统计量是否具有显著性。对于大小为 95%的置信度,Koenker(Breusch-Pagan)统计量概率小于0.05表示模型具有统计显著性。
-
Koenker(Breusch-Pagan)统计量自由度 :自由度与解释变量的个数有关,解释变量的个数越多,自由度就越大。
- Jarque-Bera统计量 :Jarque-Bera 统计量能评估模型的偏差,可用于指示残差(已知的因变量值 减去 预测值)是否呈正态分布,该检验的零假设为残差呈正态分布。当该检验的 p 值较小(如,对于大小为 95% 的置信度,其值小于 0.05),且回归呈非正态分布时,指示您的模型有偏差。如果残差还存在统计学上显著的空间自相关,则偏差可能是模型的某个关键变量缺失得到的结果,因此,该 OLS 模型得到的结果是不可信的。
- Jarque-Bera统计量的概率 :用于检验 Jarque-Bera 统计量是否具有显著性。对于大小为 95%的置信度,Jarque-Bera 统计量概率小于0.05,表示模型具有统计显著性。
- Jarque-Bera统计量自由度 :自由度与解释变量的个数有关,解释变量的个数越多,自由度就越大。
-
变量分布与关系
该部分为模型中每个解释变量的分布直方图以及因变量与每个解释变量之间关系的散点图。直方图显示了每个变量的分布方式。OLS并不要求变量呈正态分布,若您难以找到对应模型,则可尝试对偏态分布的变量进行变换以查看是否可以获得更好的结果。
散点图描述了每个解释变量和因变量之间的关系,较强的关系将呈对角线,而且倾斜方向会指示关系的正或负。散点图还可检查变量之间的非线性关系,显示哪些变量是好的预测因子。
-
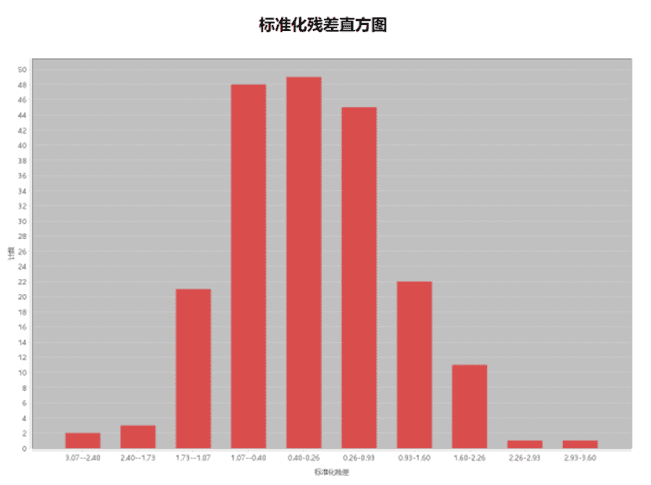
标准化残差直方图
理想情况下标准化残差直方图呈正态分布,如果直方图与标准正态分布存在明显差异,则您的模型可能有偏差。此外,还可以检查 Jarque-Bera p值来判断模型偏差,即检验的 p 值较小(如,对于大小为 95% 的置信度,其值小于 0.05),且回归呈非正态分布时,指示您的模型有偏差。
-
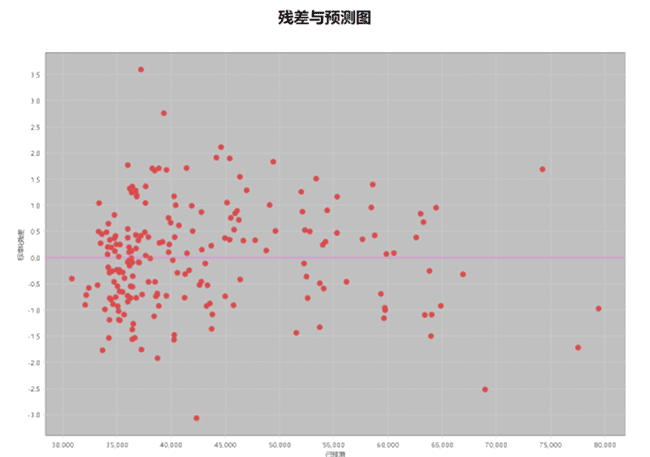
残差与预测图
散点图描述了模型残差与预测值之间的关系,显示了建模关系是否随预测的变量值而变化(异方差性)。若正在对房价进行建模,下图表示该模型可以较好地预测房价较低的地点,但不能很好地预测房价较高的地点。
模型评判
选定了因变量和候选解释变量之后,并做好了 OLS 回归分析,为了了解是否找到一个有用、稳定的模型,需要对输出的检测参数进行以下诊断。
- 哪些解释变量有显著性
- 系数 :绝对值越大,表示该变量在模型里面贡献越大;越接近于零,相关解释变量作用越小。
- 概率 :如果概率小于 0.05,表示相关解释变量对模型非常重要,其系数在 95% 置信度上具有统计显著性。
- 稳健概率 :Koenker(Breusch-Pagan)统计量的概率小于0.05时,稳健概率小于0.05,解释变量具有显著性。
-
因变量与解释变量之间的关系
解释变量系数的符号表示它与因变量之间的相关性,正值表示为正相关关系,负值表示为负相关关系。在创建候选解释变量列表时,每个变量都会有用户所期望的相关关系(正或负)。若分析结果中,有一个解释变量与因变量的关系不符合理论,而其他的检测参数均正常,则因变量可能会跟某些新原因有关,有助于改进模型的准确性。例如:分析结果表示森林火灾频率与降雨量之间存在正关系,很有可能是因为所研究的区域内森林火灾的主要原因是闪电。
-
解释变量是否为冗余变量
在进行分析时,为了构建不同因素的模式,选择的解释变量会偏多,需要了解其中是否有冗余变量。膨胀因子(VIF)是对变量冗余度的一种度量,根据经验,VIF 值超过7.5 可能为冗余变量。若有冗余变量,将其移除,重新执行OLS分析即可;若模型是用于预测,而结果的拟合性较好,也可不对冗余变量做处理。
-
模型是否出现了偏差
可用模型残差来判断模型是否出现了偏差,对模型残差字段创建直方图,若模型残差为正态分布,则表示模型准确无偏差;若模型残差非正态分布,则表示模型出现了偏差。若模型有偏差,可为模型所有解释变量创建散点图,查看是否为非线性关系或存在异常值,并可通过以下方式进行改正:
-
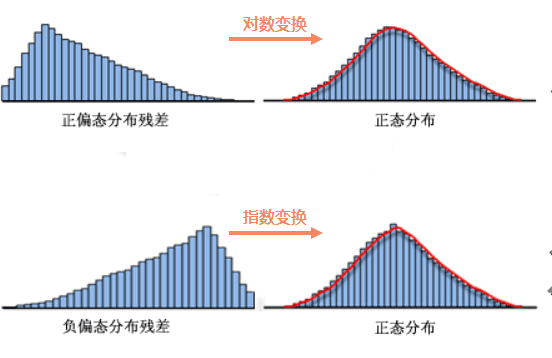
非线性关系 :这是出现模型偏差的常见原因,可采取变量变换的方式使线性关系更明显。常见变换包括对数变换和指数变换,通过解释变量直方图的分布情况来选择变换方式,如下图:
-
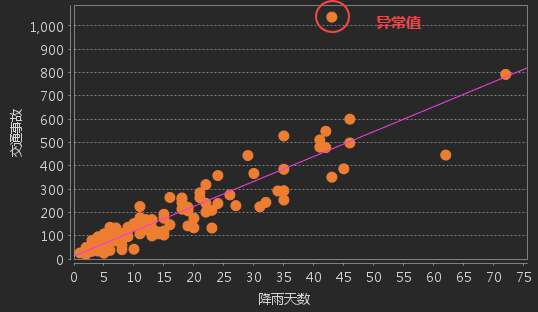
异常值 :在散点图中查看是否具有异常值,再分析异常值是否影响模型,分别在含有和不含有异常值的情况下运行 OLS,对比异常值对模型性能的更改程度,以及移除异常值是否会校正模型偏差。若异常值为错误数据,可删除异常值。
-
是否找到了所有关键解释变量
模型残差中存在统计显著性空间自相关现象,这是您丢失一个或多个关键解释变量的证据。在回归分析中,具有空间自相关残差的问题通常具有聚类的现象:偏高预计值聚集在一起,偏低预计值聚集在一起。可对残差字段进行空间自相关性分析,若结果中的P<0.05,表示您的模型丢失了关键解释变量。
-
模型性能评价
满足以上5个条件之后,可通过校正 R2 值是对模型的优劣性进行评估。R2 值的范围介于 0 和 1之间,以百分比形式表示。假设您正在为交通事故率建模,并找到一个通过之前所有五项检查的模型,其校正 R2 值为0.7。这样您就可以了解到模型中的解释变量说明交通事故率是 70%,也可理解为模型解释了交通事故率因变量中 70%的变化量)。不同领域对R2值要求i不同,在有些科学领域,能够解释复杂现象的 25% 就足以振奋人心;而某些领域,R2 值可能需要靠近 80% 才能令人满意。
AICc 值也常用于评判模型,AICc 值越小,越适合观测的数据。