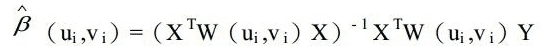回归分析可对空间关系进行建模、检查和探究,解释因变量与自变量之间的因果关系,从而可更好地理解对建模的变量产生影响的关键因素,以及对未知值进行预测。使用回归分析有以下原因:
- 找原因 :为某一种现象建模,以更好地了解引起该现象原因,分析解释变量对该现象的影响程度,应采取哪些相应措施。例如:了解某些濒危物种主要生活环境的特征,如气温、湿度、食物、捕杀、天敌),以通过相关的环境保护、法律规定等措施来协助该物种的保护。
- 预测 :根据已知的一组因变量数值,及因变量与解释变量之间的关系,来预测制定时间或地点的自变量值。例如:通过去年财政收入与工业总产值、消费品零售额、总出口以及固定资产投资的数值和关系,根据今年前半年的工业总产值、消费品零售额、总出口以及固定资产投资,可以预测前半年财政收入的情况。
- 数据挖掘 :了解或者检验两种现象是否存在正相关或者负相关的关系。例如:经济富裕的区域入室盗窃案更多还是贫穷的区域盗窃案更多呢?
回归分析的应用
可以解决以下类型的问题:为什么某一现象会持续的发生,是什么因素导致了这种情况?对某种现象建模以预测其他地点或者其他时间的数值?
回归分析方法被广泛地用于解释市场占有率、销售额、品牌偏好及市场营销效果。把两个或两个以上定距或定比例的数量关系用函数形势表示出来,就是回归分析要解决的问题。其中的一些应用示例包括:
- 对中学留校率建模以更好地了解有助于孩子们继续留在学校里读书的各种因素。
- 构建交通事故与速度、路况、天气等因素之间的函数,以便为警方提供数据参考信息,旨在降低交通事故率。
- 构建因火灾造成的财产损失与消防部门的介入程度、响应时间或财产价值等变量之间的函数。如果发现响应时间为关键因素,则表示您可能需要建造更多的消防站。如果发现介入程度为关键因素,则表示您可能需要增加设备和消防队员的数量。
分析原理
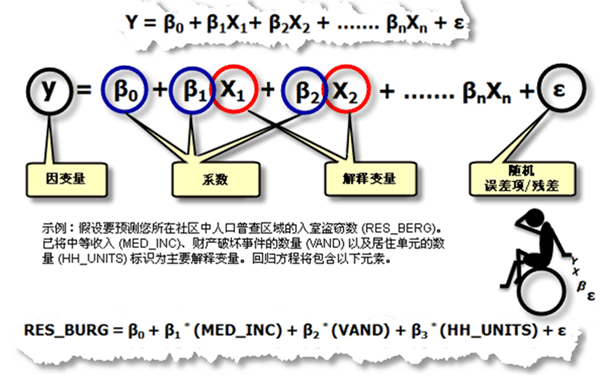
回归方程是一个可利用一个或多个解释变量对因变量进行最佳预测的数学公式。回归方程中的因变量总是标记为 y ,自变量或解释变量总是标记为 X ,这种表示方式对于那些将 x 和 y 视为坐标的地理学界的专业人员来说可能有些不便。每个自变量都与一个描述该变量与因变量之间关系强度和符号的回归系数相关联。回归方程的可能形式如下,其中,y 是因变量,X 是解释变量,β 是回归系数。
- 因变量 (y) :该变量表示您正尝试预测或了解的观测值(如:房价、入室盗窃数)。在回归方程中,因变量位于等号的左侧。构建模型时,需先给定一组已知的 y 值,然后可利用这些值来构建回归模型。
- 解释变量 (X) :即自变量,位于等号的右侧,通过这些变量用于对因变量的值进行建模或预测。例如,如果您打算预测商店每年的采购量,那么模型中可能需要使用一些解释变量来表示潜在客户的数量、与竞争对手之间的距离、店面是否显眼以及当地的消费模式。
- 回归系数 (β) :回归系数是一组数值,表示解释变量与因变量之间的关系强度和类型,每个解释变量都有一个对应的回归系数。当因变量与解释变量为正相关关系时,关联系数的符号也为正;当关系为负相关时,关联系数的符号也为负。如果关系很强,则系数也相对较大;若相关关系较弱,则关联系数接近于零。
地理加权回归分析首先要确定一个研究区域,利用每个要素的不同空间位置,去计算衰减函数,这个是一个连续的函数,有了这个衰减函数,当你把每个要素的空间位置(一般是坐标信息(x,y))和要素的值带入到这个函数里面之后,就可以得到一个权重值(β),这个值就可以带入到回归方程里面去。如下衰减函数中的W(ui,vi)是空间权重矩阵。
普通最小二乘法
在所有的回归方法中,普通最小二乘法(OLS) 最简单、最常用的方法,可为预测的变量或过程提供一个全局模型,并且创建一个回归方程来表示该过程。OLS 可输出各种重要的诊断参数,让用户了解是否已经找到一个有用的模型,计算得到的回归系数具有更好的统计性质,其线性、无偏性和有效性是最好的。 地理加权回归(GWR) 是若干空间回归方法中的一种,被越来越多地用于地理及其他学科。通过对数据集中的各要素拟合回归方程,为预测的变量或过程提供了一个局部模型。若使用得当,这些方法可提供强大且可靠的统计数据,以对线性关系进行检查和估计。
OLS 与 GWR 都为线性回归方程,回归分析可表示一个或多个变量影响另一变量中发生正相关变化或负相关变化的几率。例如,垃圾桶分布密度越高的地区,环境的清洁程度就越高,这种关系则为正相关性。
在进行回归分析时,应先从普通最小二乘法 (OLS) 开始分析,首先获得一个正确指定的 OLS 模型,然后使用同样的解释变量运行 GWR。例如,为了预测下一年的房价,可先用 OLS 进行建模,找到影响房价的重要要素,构建预测值更为准确的模型,再用GWR进行分析。
地理加权回归
地理加权回归(GWR) 是若干空间回归技术中的一种,越来越多地用于地理及其他学科。通过使回归方程适合数据集中的每个要素,地理加权回归(GWR) 可为您要尝试了解、预测的变量或过程提供局部模型。地理加权回归(GWR)构建这些独立方程的方法是:将落在每个目标要素的带宽范围内的要素的因变量和解释变量进行合并。带宽的形状和大小取决于用户输入的核类型、带宽方法、距离以及相邻点的数目参数。GWR 是一种用于建模空间变化关系的线性回归的局部形式,课解决因为地理位置的变化,而引起的变量间关系或结构的空间非平稳性。