地理加权回归是近年来提出的一种新的空间分析方法,为局部回归模型,它通过将空间结构嵌入线性回归模型中,以此来探测空间关系的非平稳性。通过回归分析,我们可以对空间关系进行建模、检查和探究,还可以解释所观测到的空间模式背后的诸多因素,还可以对这些现象进行预测。
其分析原理及应用场景可查看回归分析页面
功能入口
- 空间分析 选项卡-> 空间统计分析 组 -> 空间关系建模 -> 地理加权回归分析 。(iDesktop)
- 空间统计分析 选项卡 -> 空间关系建模 -> 地理加权回归分析 。(iDesktopX)
- 工具箱 -> 空间统计分析 -> 空间关系建模 -> 地理加权回归分析 。(iDesktopX)
主要参数
- 源数据 :设置待分析的矢量数据集,支持点、线、面三种类型的数据集。注意:源数据中的对象个数要大于20。
- 解释字段 :解释变量是自变量,即回归方程里面的X,用于对因变量的值进行建模或预测。例如,我们想研究肥胖的诸多原因,想找到肥胖与收入、健康食品摄入、教育水平等因素是否有关联。在这个例子中,肥胖就是因变量(Y),收入、健康食品摄入、教育水平等这些因素即为解释变量(X)。
-
核函数类型 :设置两点之间距离权重的计算函数类型,支持以下五种核函数类型,各函数计算公式中:Wij为点i和点j之间的权重。dij为点i和点j之间的距离,b为带宽范围。
- 二次核函数:如果dij≤b,Wij=(1-(dij/b)^2))^2;否则 Wij=0。
- 盒状核函数:如果dij≤b, Wij=1;否则 W_ij=0。
- 高斯核函数:计算公式为:Wij=e^(-((dij/b)^2)/2)。
- 立方体核函数:如果dij≤b, Wij=(1-(dij/b)^3))^3;否则 Wij=0。
- 建模字段 :因变量,即待研究、预测的变量,只支持数值字段。
-
带宽方式 :设置分析带宽范围的确定方式,支持以下三种确定方式:
- Akaike 信息准则(AICc):使用Akaike 信息准则 (AICc)确定带宽范围,适用于不确定距离或相邻要素的数目参数的情况下使用。
- 交叉验证:使用交叉验证的方式确定带宽范围,交叉验证在回归系数估计时,不包括回归点本身,即只根据回归点周围的数据点进行回归计算。该值就是每个回归点在交叉验证中得到的估计值与实际值之差,它们的平方和为CV值。适用于不确定距离或相邻要素的数目参数的情况下使用。
- 固定距离或相邻数:根据固定距离或固定相邻数确定带宽范围,必须设置距离或相邻要素数量的值。
-
带宽类型 :提供了固定型带宽和可变型带宽两种:
- 固定型带宽:若用户选择的带宽方式是固定距离或相邻数,则需要设置“带宽范围”,指定一个值为固定距离;若用户选择的带宽方式是AICc或交叉验证,用户不需要指定距离,程序可根据数据计算一个固定距离值。
- 可变型带宽:若用户选择的带宽方式是可变距离或相邻数,则需要设置“相邻数目”,应用程序会根据回归点与最近相邻点之间的距离作为带宽范围;若用户选择的带宽方式是AICc或交叉验证,用户不需要指定相邻数目,程序可根据数据找到相邻点并计算一个固定距离值。
- 结果设置 :设置结果数据所要保存在的数据源,及数据集名称。
结果输出
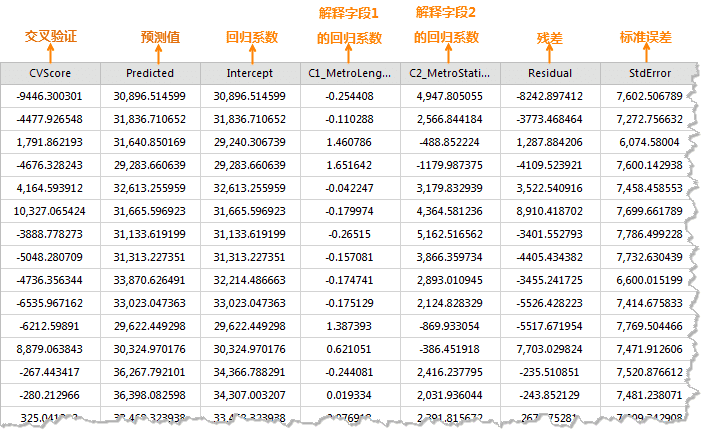
设置好以上参数后,单击对话框中的“确定”按钮,即可执行地理加权回归分析,结果数据集包含结果属性字段:交叉验证(CVScore)、预测值(Predicted)、回归系数(Intercept、C1/解释字段名)、残差(Residual)、标准误差(StdError)、系数标准误差(SE/Intercept、SE1/解释字段名)、伪t值(TVIntercept、TV1_解释字段名)和Studentised残差(StdResidual)。如下图所示:
- 交叉验证(CVScore):该值就是每个回归点在交叉验证中得到的估计值与实际值之差,它们的平方和为CV值。作为一个模型性能指标。
- 预测值(Predicted):这些值是地理加权回归得到的估计值(或拟合值)。
- 回归系数(Intercept):它是地理加权回归模型的回归系数,为回归模型的回归截距,表示所有解释变量均为零时因变量的预测值。
- 回归系数(C1_ _解释字段名):它是解释字段的回归系数,表示解释变量与因变量之间的关系强度和类型。如果回归系数为正,则解释变量与因变量之间的关系为正向的;反之,则存在负向关系。如果关系很强,则回归系数也相对较大;关系较弱时,则回归系数接近于0。
- 残差(Residual):这些是因变量无法解释的部分,是估计值和实际值之差,标准化残差的平均值为0,标准差为1。残差可用于确定模型的拟合程度,残差较小表明模型拟合效果较好,可以解释大部分预测值,说明这个回归方程是有效的。
- 标准误差(StdError):估计值的标准误差,用于衡量每个估计值的可靠性。较小的标准误差表明拟合值与实际值的差异程度越小,模型拟合效果越好。
- 系数标准误差(SEIntercept、SE1 _解释字段名):这些值用于衡量每个回归系数估计值的可靠性。系数的标准误差与实际系数相比较小时,估计值的可信度会更高。较大的标准误差可能表示存在局部多重共线性问题。
- 伪t值(TVIntercept、TV1 _解释字段名):是对各个回归系数的显著性检验。当T值大于临界值时,拒绝零假设,回归系数显著即回归系估计值是可靠的;当T值小于临界值时,则接受零假设,回归系数不显著。
- Studentised 残差(StdResidual):残差和标准误差的比值,该值可用来判断数据是否异常,若数据都在(-2,2)区间内,表明数据具有正态性和方差齐性;若数据超出(-2,2)区间,表明该数据为异常数据,无方差齐性和正态性。
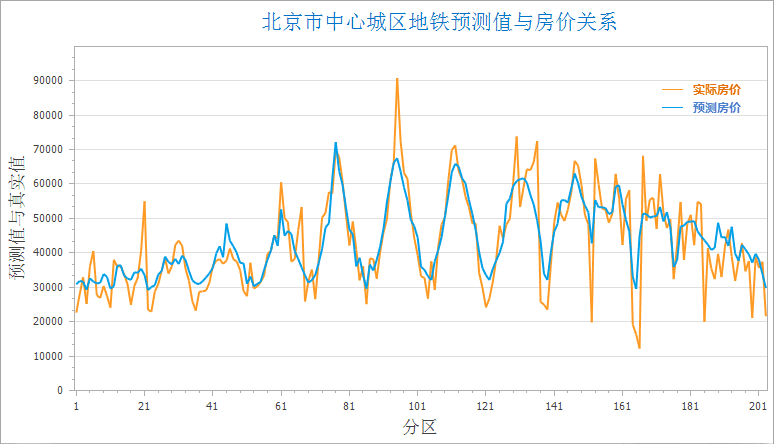
下图为地理加权回归分析的预测值与实际值的对比图,根据2016年北京市中心城区的房价,以周围的地铁站个数和地铁线路长度为解释变量,模拟出2016年北京市中心城区的房价,下图中的橘色线为实际房价蓝色线为拟合房价。
执行成功后,输出窗口会输出本次分析的结果信息,如下图所示。若分析结果的残差在用户的接受范围内,即可根据该结果及解释变量,预测事件的结果。
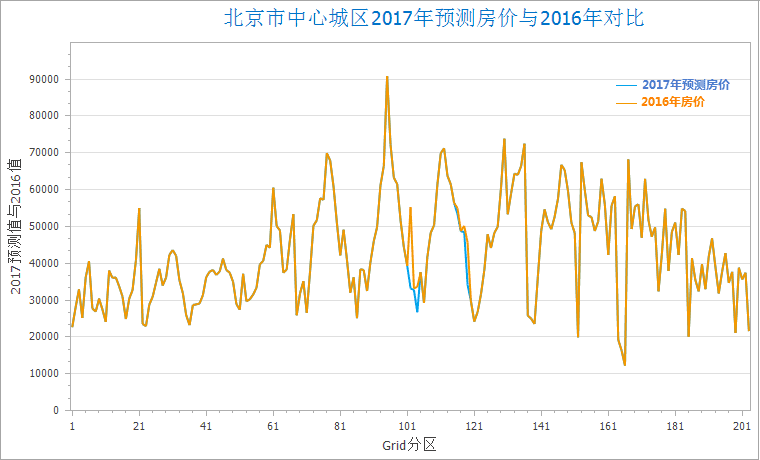
此时,可根据地理加权回归分析的结果属性值及2017年新增的地铁站和地铁线路长度,对2017年北京市中心城区的房价进行预测,计算公式为:2017预测房价 = Intercept(回归系数) + C1(解释字段1回归系数) * 2017地铁站 + C2(解释字段2回归系数) * 2017地铁线长度。根据该公式可根据地铁的变化信息,预测北京中心城区2017年的房价,结果如下图所示,从结果图中可知,地铁线路有变化的地区房价又有一定的波动。