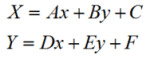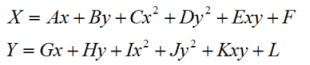Four algorithms are provided for registering data including: Linear, Polynomial, Rectangular and Offset. Following contents introduce the four algorithm and related concepts.
- Linear
It is also called affine transformation. This registration algorithm supposes the actual scales are different in direction X and direction Y because of the deformation, therefore, it has the functionality of rectifying the map deformation. Suppose that x and y are original coordinates of the input image, and X and Y are output coordinates after rectification, then the formula of coordinate transformation is as follows:
There are 6 parameters in the above formula: A, B, C, D, E, F, which can be determined by selecting identically named control points in the registration layer and reference layer. Theoretically if you want to solve the above 6 parameters, you should know the coordinates of at least 3 pairs of control points that are not on the same line so that the linear transformation can be implemented. If the constant parameter C and F are set to 0, then at least 4 points are required. In practical applications, usually no less than 4 control points are used to implement linear registration. The parameters to be determined are solved by the principle of least square method.
The linear transformation is a commonly used registration method. The deformations in direction X and direction Y are considered simultaneously, therefore, the coordinates after rectification will have different length ratios in different directions, with the performance that the original coordinates will experience changes such as zooming, rotating, panning and then get the output coordinates.
- Polynomial
It is a commonly used registration method with a relatively high accuracy. The polynomial rectification regards the original image deformation as a kind of curved surface, and the output image is a regular surface. Theoretically speaking, any curved surface can be fit by suitably high-order polynomials. Generally, quadratic binomial is sufficient to implement rectification for the image with relatively serious deformations, and get a relatively high accuracy. The rectification formula of the quadratic binomial is as follows:
There are 12 parameters in the above formula. Theoretically 6 pairs of control points are sufficient to implement the transformation. However, it generally requires at least 7 pairs of control points in order to get a relatively high accuracy. Adding the number of control points properly can improve the accuracy of image registration notably. The polynomial coefficients are obtained using the coordinates of selected control points according to the least square method. Comparing the formula of polynomial rectification with the formula of linear rectification, it can be seen that the linear registration is in fact a first-order polynomial registration. The quadratic polynomial rectification needs more control point pairs than the linear registration, and can also rectify more deformations.
- Rectangular
It is in fact a special linear registration with limitations. If the original image is a regular rectangle, and the image coordinate after rectification is also a regular rectangle, then selecting 2 opposite corner points can determine the coordinates of 4 corner points of the rectangle. Set the constant in the rectification formula to 0, then the rectification formula can be solved with the known coordinates of the 2 opposite corner points. This method is convenient and time-saving, and also avoids the error accumulation caused by selecting multiple control points. The rectangular registration is a simple and convenient registration rectification method. However, the output result cannot calculate errors, therefore, its registration accuracy cannot be known, and it is a coarse rectification method with an accuracy that is not high.
- Offset
The offset registration requires only one group of control points and reference points. It calculates the difference for the coordinate X and coordinate Y respectively, and then uses the difference to implement the offsets for all groups of coordinate points of the original dataset.
Note
- The offset registration doesn’t support error calculation. The grid data does not support the offset registration method. The offset registration method does not need error calculation. In fact, the registration is implemented by implementing offsets in directions of x axis and y axis respectively through calculating the differences of x coordinate and y coordinate between the source point and the target point.