The median center function identifies the location that minimizes overall Euclidean distance to the features in a dataset. The result is a new point rather than an object from the source dataset.
Both mean center and median center measure central tendency. However, the median center is less sensitive to extremes (outliers) compared to the mean center. For example, calculating the mean center for a compact cluster of points yields a location at the cluster's center. If a new point far from the cluster is added and the mean center recalculated, the result shifts toward the new outlier. In contrast, repeating this test with the median center tool shows significantly reduced impact from the outlier on the resulting location.
While both median center and central feature seek the point with the minimal total distance to other features, they differ in implementation: the central feature result must be an original sample from the input features, whereas the median center can generate a new location outside the original dataset.
Feature Entry
- Spatial Statistics Tab -> Measuring Geographic Distributions -> Median Center.
- Toolbox->Spatial Statistics->Measuring Geographic Distributions->Median Center.
Parameter Description
- Source Dataset: Specifies the vector dataset to be analyzed, supporting point, line, or polygon datasets. For line/polygon objects, their centroids will be used for calculation. Points have a weight of 1, lines are weighted by length, and polygons by area.
- Group Field: A field to categorize features. Each group will generate a separate median center. Accepts integer, date, or string types. Features with empty group field values will be excluded.
- Weight Field: Applies weights when calculating distances between features. Weighted distance formula: D = W1 × d, where W1 is the weight value and d is the Euclidean distance.
- Mean Center: Configures reserved fields and statistical types for result data in the field list.
- Result Settings: Specifies the output datasource and dataset name for storing results.
After configuring parameters, click the OK button in the dialog to execute the median center analysis.
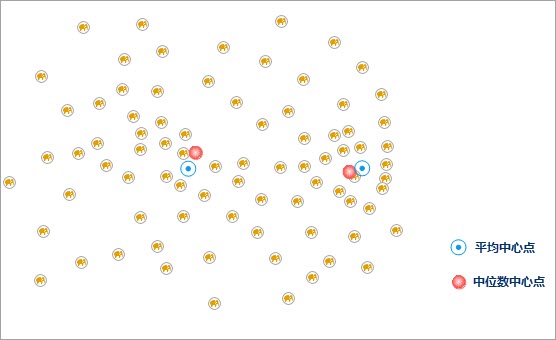
As illustrated below: Yellow points represent seasonal activity locations of elephants in a wildlife park. Calculating the median center helps determine their aggregation areas, providing better position information for visitors.
Related Topics



