Defines constants for data registration.

There are four methods for data registration:linear registration (affine transformation), rectangle registration, polynomial equations and offset registration.

Linear registration, also called affine transformation, is expressed as a pair of linear equations:

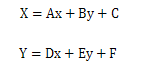
Where x, y are in the original coordinates, X, Y are in real-world coordinates, and A, B, C, D, E, and F are the transformation coefficients. The six coefficients can be estimated by using the original coordinates and the real-world coordinates of the selected control points. A minimum of three pairs of control points is sufficient for the estimation. But often four or more pair of control points are used to reduce problems in measurement errors. With four or more pair of control points, a least squares solution is used to estimate the transformation coefficients. After the coefficients are estimated, the transformation equations are applied to the map features in the source map and convert their original coordinates to real-world coordinates.

Rectangle registration is a simplified linear registration. If the source image and the result map are both regular rectangle, then by identifying the coordinates of the two points on one diagonal, the coordinates of the two points on the other diagonal can be calculated. By using the two affine transformation equations with constant coefficients C and F set to 0, the transformation can be completed easily. Because errors are not calculated in this method, it is used for rectification without much demand on the precision.

Polynomial equations are a common method used to perform precise transformation on remotely sensed image. A polynomial equation provides a mathematical model for differential scaling and rotating across an image. The degree of complexity of the model is expressed by the order of the polynomial, which may range from 2 to 5. The 2nd order polynomial is usually used, as shown below:

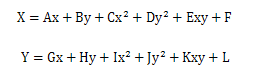
The coefficients A-L can be estimated by a minimum of 6 pairs of control points. Generally, 7 pairs of control points are used to achieve a higher precision. Also, a least squares solution is used to estimate these coefficients.

Offset registration:it only needs one set of control point and reference point, get the different value of x and y respectively, then offset all the coordinates based on the different value.