Conversion Models and Scope of Application

SuperMap desktop products support five types of coordinate transformation models: Position Vector (7-para) (Position Vector Transformation), Coordinate Frame (7-para) (Coordinate Frame Rotation Transformation), China_3D_7P (7-para) (3D Seven-Parameter Transformation Model), China_2D_7P (7-para) (2D Seven-Parameter Transformation Model), and China_2D_4P (4-para) (2D Four-Parameter Transformation Model).

Conversion Models

Position Vector (7-para), Coordinate Frame (7-para): These two methods are commonly known as seven-parameter transformations or Bursa-Wolf models, including three translation parameters, three rotation parameters, and one scale factor. They can be considered as variants of the same model, differing only in sign conventions for rotation parameters defined by different countries.

Position Vector (Position Vector Transformation): European convention with counterclockwise rotation as negative.
Coordinate Frame (Coordinate Frame Rotation Transformation): US and Australian convention with counterclockwise rotation as positive.

China_3D_7P (7-para): The 3D seven-parameter transformation model is used for geodetic coordinate conversion between different ellipsoid datums. It includes three translation parameters, three rotation parameters, and one scale factor, while considering differences in semi-major axis and flattening between the two reference ellipsoids.
China_2D_7P (7-para): The 2D seven-parameter transformation model is used for converting geocentric coordinates to geodetic coordinates under different ellipsoid datums, involving three translation parameters, three rotation parameters, and one scale factor.
China_2D_4P (4-para): The 2D four-parameter transformation model is used for planar coordinate conversion between different Gauss projection zones within local areas. It includes two translation parameters, one rotation parameter, and one scale factor. For 3D coordinates, planar coordinates should first be obtained through Gauss projection before calculating transformation parameters.

Scope of Application

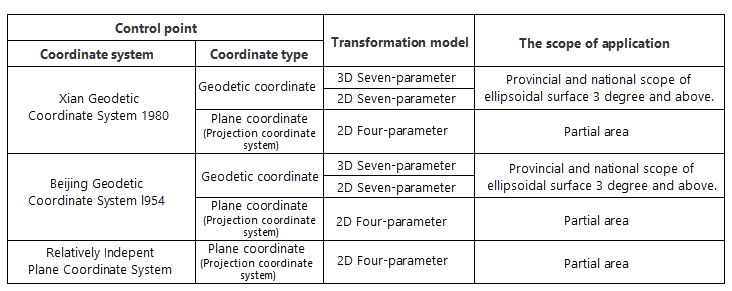
The selection of transformation models depends on control point coordinate systems and conversion areas. Users should refer to the applicable scopes specified in the Technical Specifications for Geodetic Control Point Coordinate Transformation, choosing appropriate models based on source data coordinate systems and regional applicability.

Position Vector (7-para), Coordinate Frame (7-para): Applicable for coordinate transformation of control points in provincial and national areas using space rectangular coordinates.
China_3D_7P (7-para): Suitable for geodetic coordinate transformation of control points in provincial and national areas with ellipsoid coverage exceeding 3°.
China_2D_7P (7-para): Suitable for geocentric coordinate transformation of control points in provincial and national areas with ellipsoid coverage exceeding 3°.
China_2D_4P (4-para): Designed for small-area planar coordinate transformation of control points and establishing connections between independent planar coordinate systems and the China Geodetic Coordinate System 2000 (CGCS2000).

The following table shows model selection and application scopes for transforming control points from different coordinate systems to CGCS2000:

Application Scenarios

SuperMap desktop users can convert local coordinate system data to CGCS2000 without third-party plugins, achieving transformation results across different coordinate systems.

For local coordinate systems derived from offset general coordinate systems (e.g., Xian1980, Beijing1954): Conversion to CGCS2000 requires two steps:

Step 1: Convert local system to general coordinate system: Use the "Reproject Dataset" function with the China_2D_4P model.

Step 2: Convert general system to CGCS2000: Calculate parameters using "Calculate Transformation Parameters", then apply models like China_2D_7P, China_3D_7P, or Coordinate Frame via "Reproject Dataset".

For local systems based on actual projection zones: Directly implement Step 2 for conversion to CGCS2000.

Model Formulas

Position Vector (7-para), Coordinate Frame (7-para)

China_3D_7P (7-para)

China_2D_7P (7-para)

China_2D_4P (4-para)

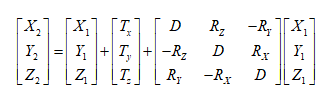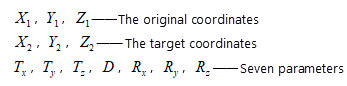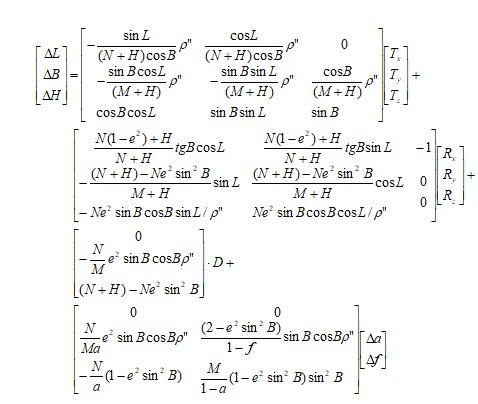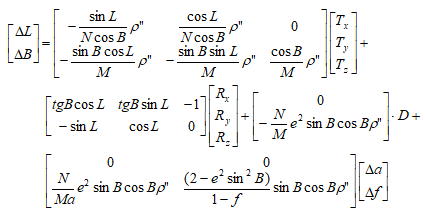Notes:

When working with Gauss-Krüger projected coordinate systems, note that coordinate values (Y,X) in projection systems will be displayed as (X,Y) in applications.