Ordinary Least Squares

Ordinary Least Squares (Ordinary Least Square, OLS) is one of the simplest and most widely used regression methods. OLS provides a global model for a variable or process that the user wants to understand/predict; it also creates a single regression equation that represents the process. Geographically weighted regression (GWR) is one of several spatial regression methods that are increasingly used in geography and other disciplines. By fitting a regression equation to each element in the Dataset, GWR provides a local model for the variable or process that the user wants to understand/predict.

Function entrance

  • Spatial Statistical Analysis tab-> Spatial Relationship Modeling-> Ordinary Least Squares. （iDesktopX）
  • Toolbox-> Spatial Statistical Analysis-> Spatial Relationship Modeling-> Ordinary Least Squares. （iDesktopX）

Main parameters

  • Source Data: Set the Vector Dataset to be analyzed, which supports three types of Dataset: point, line and surface. Note: The Object Count in the Source Dataset should be greater than 3.
  • Explanatory variable: The explanatory variable is the independent variable, that is, the X on the right side of the regression equation. One or more numerical fields can be checked as the explanatory variable to model or predict the value of the dependent variable. Note: If the values of an explanatory variable are all equal, the regression equation of OLS cannot be solved.
  • Modeling field: the dependent variable, the variable to be studied or predicted, which is located on the left side of the regression equation and only supports numerical fields. It is necessary to construct a regression model based on the known observed values to obtain the predicted dependent variables.
  • Result Data: Set the Datasource and Dataset Name where the Result Data is to be saved, which is consistent with the Data Type of the source data.

Result output

The Predicted value, residual, and Standardized Residual in the Analyst Result of the Ordinary Least Squares are recorded in the Property Field of the Result Dataset. The Statistics Results of the OLS model, such as Distribution Statistic, Statistic Probability, AICc, and Coefficient of Determination, are displayed in the OLS report. Analyst Result is described as follows:

Results in Property Sheet

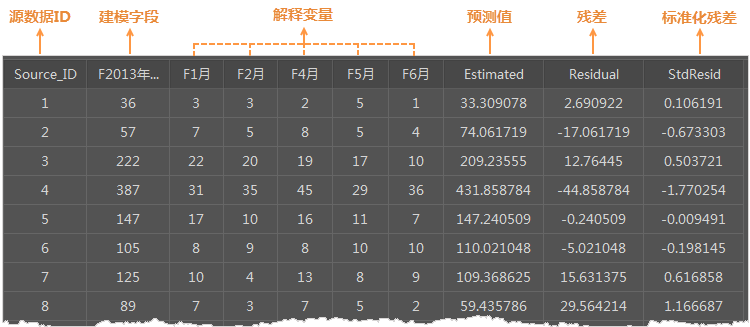
  • Source _ ID: SmID value of the object in Source Dataset, i.e. Unique Identification of the object
  • Modeling Fields and Explanatory Fields:: The modeling fields and Explanatory Fields: in the source data are retained.
  • Estimated: the fitted value obtained by OLS analysis based on the specified explanatory variables.
  • Residual: These are the unexplained portions of the dependent variable, which are the difference between the estimated and actual values. Standardized Residual has a mean of 0 and a standard deviation of 1. Residuals can be used to determine the degree of fit of the model. A small residual indicates that the model fits well and can explain most of the predicted values, indicating that the regression equation is valid. Spatial Autocorrelation analysis can be performed on the residuals, and if the statistical significance of high or low residuals is clustered, it indicates that a key variable in the model is missing. The OLS results are not credible at this time.
  • StdResid: Standard residual error is the ratio of residual error to Standard Errors, which can be used to judge whether the data is abnormal. If the standard residuals are normally distributed, it means that the performance of the model is excellent; if there is a serious skew, it means that the model is biased, and one of the key variables of the model may be missing. If the data are all in the interval of (-2,2), it indicates that the data have normality and homogeneity of variance; if the data are beyond the interval of (-2,2), it indicates that the data are abnormal data without homogeneity of variance and normality.

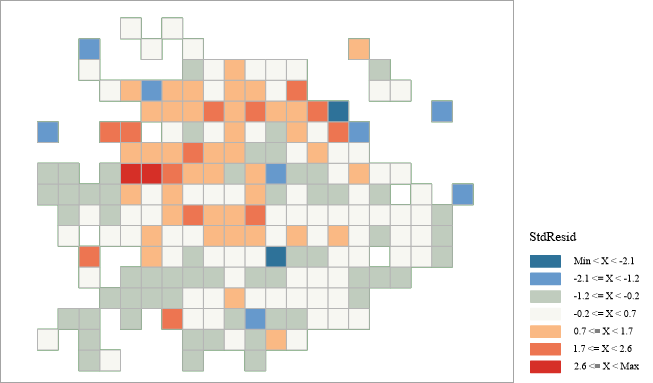
Model residual visualization

At the end of the execution, the model residual Graudated Colors Map will be generated in Map. The high or low predictive value of the correct regression model is Random Distribution. If the high or low predictive value is Clustering Distribution, it means that at least the key explanatory variables are lost. Examine the distribution of model residuals to see what explanatory variables may be missing from these cluster regions from the characteristics of the residual distribution. Sometimes, performing a Hotspot Analysis on the model residuals can help you determine how the residuals are distributed.

OLS Report

After the execution, an OLS report will be generated in the Output Window, in which the OLSAnalyst Result is recorded in detail. Model variables, model significance analysis, Variable Distribution and Relationship, Standardized Residual Histogram, and scatter plots of residuals and predicted values were included. Details are as follows:

  • Model Variables

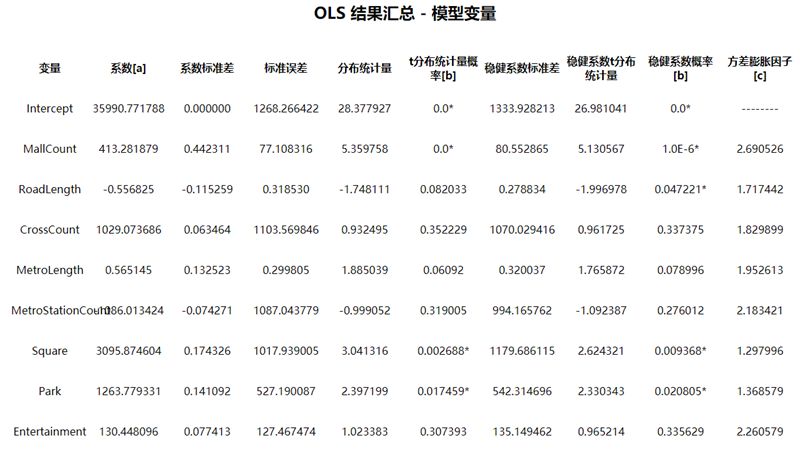
    • Coefficient: The coefficient reflects the strength and type of relationship between each explanatory variable and the dependent variable. The greater the absolute value of the coefficient, the greater the contribution of the variable in the model, and the closer the relationship between the explanatory variable and the dependent variable. The coefficient reflects the expected amount of change that would occur in the dependent variable for each unit change in the associated explanatory variable if all other explanatory variables were held constant. For example, keeping the other explanatory variables constant, the burglary coefficient increases by 0.005 for each additional person in the census block. At the same time, the coefficient also indicates the type of relationship between the explanatory variable and the dependent variable. A positive coefficient indicates a positive correlation, for example, the greater the population, the greater the number of burglaries. A negative coefficient indicates a negative correlation, for example, the greater the distance from the town center, the less the number of burglaries.
    • Coefficient Standard Errors: indicates the degree of dispersion of different explanatory variables.
    • Standard Errors: These values are used to measure the reliability of each coefficient estimate. The smaller the Standard Errors, the greater the confidence in the model estimates; larger Standard Errors may indicate problems with local multicollinearity.
    • Distribution Statistic: used to evaluate whether an explanatory variable is statistically significant, t-Statistic = Mean/Standard Errors. Generally speaking, this value is similar to P-value in meaning, which is the significance of the model in the case of verifying the null hypothesis, but sometimes P-value will have some problems, such as losing some information. When statistical verification is carried out in the computer, the larger the t statistic is, the more significant it is.
    • Probability: When the probability p is very small, the probability that the coefficient is actually zero is also very small.
    • Robust Coefficient Standard Errors: It is to see whether the regression coefficients and results of the explanatory variables concerned are robust by modifying (adding or deleting) the variable values.
    • Robust Coefficient: used to evaluate whether the robust coefficient is statistically significant.
    • Robust Coefficient Probability: If Koenker (Breusch-Pagan) is statistically significant, robust probabilities should be used to assess the statistical significance of the explanatory variables.
    • Variance Inflation Factor: Variance Inflation Factor (VIF). This value mainly verifies whether there are redundant variables in the explanatory variables (that is, whether there is multicollinearity). In general, as long as the Variance Inflation Factor exceeds 7.5, it indicates that the variable is likely to be redundant.
  • Model significance

    • AIC: It is a standard to measure the goodness of model fitting. It can balance the complexity of the estimated model and the goodness of the model fitting data. It takes into account the simplicity and accuracy when evaluating the model. It is shown that increasing the number of free parameters improves the goodness of fit, and AIC encourages the fit of data, but over-fitting should be avoided as far as possible. Therefore, the priority is to find the model that can explain the data best but contains the fewest free parameters with the smaller AIC value.
    • AICc (Akaike): AICc converges to AIC when the data increases, which is also a measure of model performance and helps to compare different regression models. Considering the complexity of the model, the model with lower AICc value can better fit the observed data. AICc is not an absolute measure of goodness of fit, but is useful for comparing models for the same dependent variable with different explanatory variables. If the AICc values of the two models differ by more than 3, the model with the lower AICc value will be considered the better model.
    • Coefficient of determination (R2 ): The coefficient of determination is a measure of the degree of fit, and its value varies between 0.0 and 1.0. The larger the value, the better the model. R2 can be interpreted as the proportion of the variance of the dependent variable covered by the regression model. The denominator of the R2 calculation is the sum of the squares of the values of the dependent variables. Adding an explanatory variable will not change the denominator but will change the numerator. This will appear to improve the fit of the model, but may also be an artifact.
    • Corrected R-squared: The calculation of the corrected R-squared normalizes the numerator and denominator degrees of freedom. This has the effect of compensating for the number of variables in the model, since the corrected R2 value is usually smaller than R2 value. However, this value cannot be interpreted as a proportion of the explained variance when the correction is performed. The effective number of degrees of freedom is a function of bandwidth, so AICc is the preferred way to compare models. The values of

      these two coefficients are between 0 and 1, which can be converted into percentages, usually referring to the explanatory power of the independent variable equation to the dependent variable. For example, when it is equal to 0.8, it means that the regression equation can explain 80% of the changes in the dependent variable. The higher the square coefficient is, the higher the coincidence degree is. The correction R-square coefficient is usually slightly lower than multiple R-square coefficient, because the technology of this coefficient is more related to the data situation, so the performance evaluation of the model is more accurate.

    • Joint F-statistic: The joint F-statistic is used to test the statistical significance of the entire model. The joint F-statistic can only be trusted if the Koenker (Breusch-Pagan) statistic is not statistically significant. The null hypothesis of the test is that the explanatory variables in the model do not play a role. For a size of 95% confidence, a joint F-statistic probability of less than 0.05 indicates that the model is statistically significant.
    • Probability of the joint F-statistic: Used to test whether the joint F-statistic is significant. For a size of 95% confidence, a joint F-statistic probability of less than 0.05 indicates that the model is statistically significant.
    • Joint F-statistic degree of freedom: The degree of freedom is related to the number of explanatory variables. The more the number of explanatory variables, the greater the degree of freedom.
    • Joint chi-square statistic: The joint chi-square statistic is used to test the statistical significance of the entire model. The joint F-statistic can only be trusted if the Koenker (Breusch-Pagan) statistic is statistically significant. The null hypothesis of the test is that the explanatory variables in the model do not play a role. For a size of 95% confidence, a joint F-statistic probability of less than 0.05 indicates that the model is statistically significant.
    • Probability of the joint chi-square statistic: Used to test whether the Koenker (Breusch-Pagan) statistic is significant. For a size of 95% confidence, a Koenker (Breusch-Pagan) statistic probability of less than 0.05 indicates that the model is statistically significant.
    • Degree of freedom of joint chi-square statistics: The degree of freedom is related to the number of explanatory variables. The more the number of explanatory variables, the greater the degree of freedom. The more degrees of freedom in the chi-square distribution, the closer the chi-square distribution is to the normal distribution.
    • Koenker (Breusch-Pagan) statistic: Koenker's standardized Breusch-Pagan statistic, which evaluates the steady state of the model and is used to determine whether the explanatory variables of the model have a consistent relationship with the dependent variable in both geographic and data space. The null hypothesis of the test is that the tested model is stationary. With a 95% confidence in size, a probability of the Koenker (Breusch-Pagan) statistic of less than 0.05 indicates that the model has statistically significant heteroscedasticity or is non-stationary. When the test result is significant, it is necessary to refer to Robust Coefficient Standard Errors and probability to evaluate the effect of each explanatory variable.
    • Probability of the Koenker (Breusch-Pagan) statistic: Used to test whether the Koenker (Breusch-Pagan) statistic is significant. For a size of 95% confidence, a Koenker (Breusch-Pagan) statistic probability of less than 0.05 indicates that the model is statistically significant.
    • The degree of freedom of Koenker (Breusch-Pagan) statistic: The degree of freedom is related to the number of explanatory variables. The more the number of explanatory variables, the greater the degree of freedom.

    • Jarque-Bera statistic: The Jarque-Bera statistic evaluates the bias of the model and can be used to indicate whether the residuals (known dependent variable values minus predicted values) are normally distributed. The null hypothesis of this test is that the residuals are normally distributed. When the p-value of the test is small (e.g., less than 0.05 for a 95% confidence level) and the regression is non-normally distributed, it indicates that your model is biased. If there is also a statistically significant Spatial Autocorrelation in the residual error, the bias may be the result of the absence of a key variable in the model, and therefore, the results obtained by the OLS model are not credible.
    • Probability of the Jarque-Bera statistic: Used to test whether the Jarque-Bera statistic is significant. For a size of 95% confidence, the Jarque-Bera statistic probability is less than 0.05, indicating that the model is statistically significant.
    • The degree of freedom of Jarque-Bera statistic: The degree of freedom is related to the number of explanatory variables. The more the number of explanatory variables, the greater the degree of freedom.
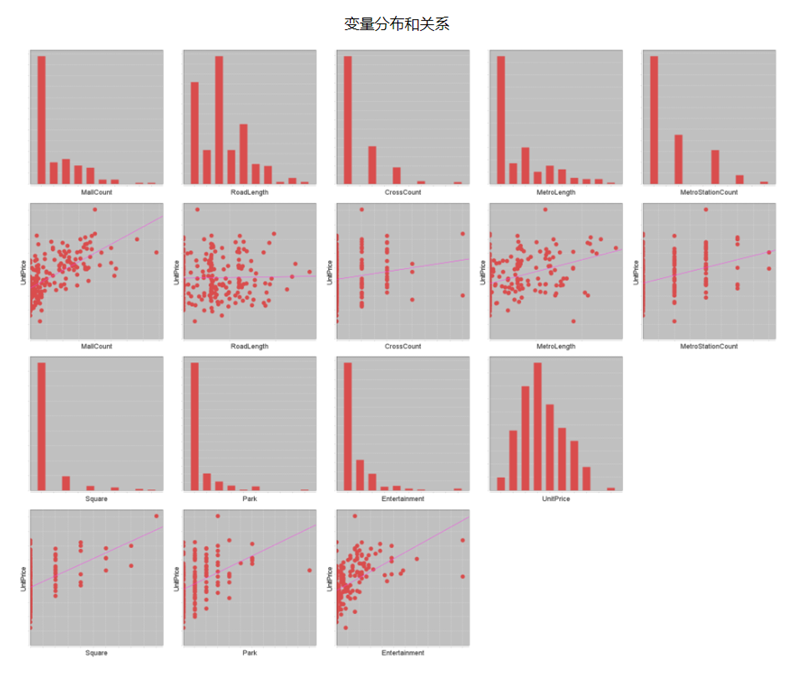
  • Variable Distribution and Relationship

    This part is the distribution histogram of each explanatory variable in the model and the scatter plot of the relationship between the dependent variable and each explanatory variable. The histogram shows how each variable is distributed. OLS does not require the variables to be normally distributed. If you have difficulty finding a model, try transforming the skewed variables to see if you can get better results.

    A scatter plot depicts the relationship between each explanatory variable and the dependent variable. A strong relationship will be diagonal, and the direction of the slope will indicate whether the relationship is positive or negative. Scatter plots can also examine non-linear relationships between variables, showing which variables are good predictors.

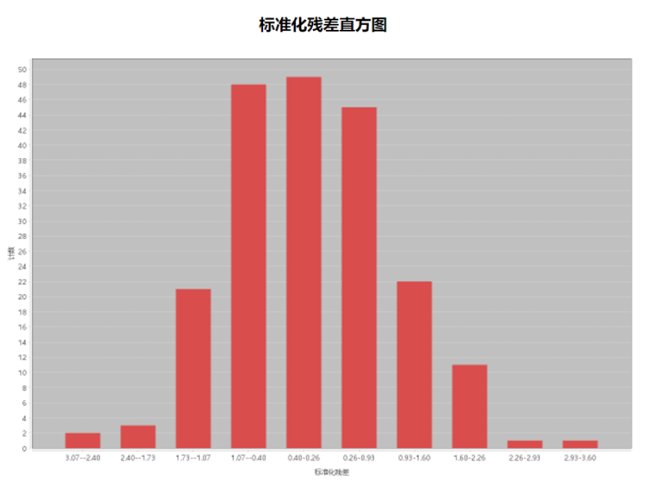
  • Standardized Residual Histogram Ideally, the

    Standardized Residual Histogram is normally distributed. If the histogram is significantly different from a standard normal distribution, your model may be biased. You can also check the Jarque-Bera p-value for model bias, i.e., when the p-value of the test is small (e.g., less than 0.05 for a size of 95% confidence) and the regression is non-normally distributed, it indicates that your model is biased.

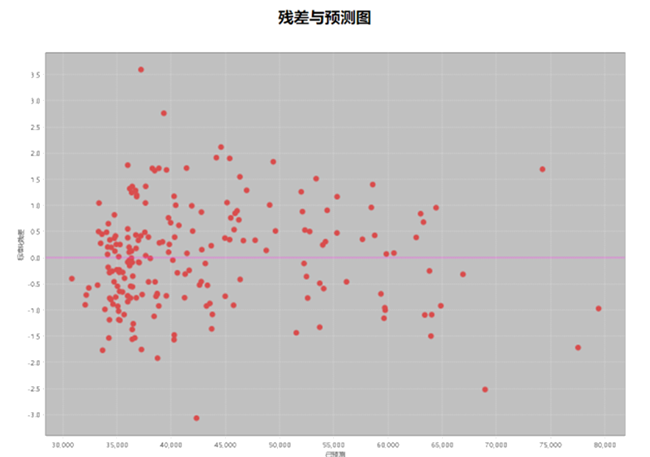
  • Residual vs Prediction Graph

    The scatter plot depicts the relationship between the model residuals and the predicted values, showing whether the modeled relationship varies with the predicted variable values (heteroscedasticity). If you are modeling house prices, the following figure shows that the model does a good job of predicting locations with low house prices, but does not do a good job of predicting locations with high house prices.

Model evaluation

After selecting the dependent variable and the candidate explanatory variable, and performing the OLS regression analysis, in order to know whether a useful and stable model is found, the following diagnosis is needed for the output Detection parameters.

  1. Which explanatory variables are significant
    • Coefficient: the greater the absolute value is, the greater the contribution of the variable in the model is; the closer to zero, the smaller the role of the relevant explanatory variables is.
    • Probability: If the probability is less than 0.05, it means that the relevant explanatory variable is very important to the model, and its coefficient is statistically significant at 95% confidence level.
    • Robust probability: When the probability of the Koenker (Breusch-Pagan) statistic is less than 0.05, the robust probability is less than 0.05, and the explanatory variable is significant.
  2. Relationship between dependent and explanatory variables The sign of the coefficient of

    an explanatory variable indicates the correlation between it and the dependent variable, with positive values indicating a positive relationship and negative values indicating a negative relationship. When creating a candidate explanation Variable List, each variable will have the correlation (positive or negative) that the user expects. If the relationship between one explanatory variable and the dependent variable in the Analyst Result is not in line with the theory, while the other Detection parameters are normal, the dependent variable may be related to some new reasons, which is helpful to improve the accuracy of the model. For example, Analyst Result indicates that there is a positive relationship between forest fire frequency and rainfall, most likely because lightning is the main cause of forest fires in the study area.

  3. Whether the explanatory variable is a redundant variable

    In the analysis, in order to construct the model of different factors, more explanatory variables will be selected, and it is necessary to know whether there are redundant variables. The inflation factor (VIF) is a measure of the redundancy of variables, and as a rule of thumb, VIF values over 7.5 may be redundant variables. If there are redundant variables, they can be removed and the OLS analysis can be performed again; if the model is used for prediction and the fitting of the results is good, the redundant variables can not be processed.

  4. Is the model biased? The model residual

    can be used to judge whether the model has a deviation. For the model residual field Create Histogram, if the model residual is normally distributed, it means that the model is accurate without deviation; if the model residual is not normally distributed, it means that the model has a deviation. If the model is biased, a scatter plot can be created for all the explanatory variables of the model to see if there is a nonlinear relationship or if there are outliers, which can be corrected by:

    • Nonlinear relationship: This is a common cause of model deviation, and the linear relationship can be made more obvious by means of variable transformation. Common transformations include logarithmic transformation and exponential transformation. The transformation mode is selected by explaining the distribution of variable histograms, as shown in the following figure:

    • Outliers: Look for outliers in the scatter plot, analyze whether the outliers affect the model, run OLS with and without outliers, compare how much the outliers change the performance of the model, and whether removing the outliers corrects the model bias. If the outlier is erroneous data, the outlier can be deleted.

  5. Are all key explanatory variables found? There is a statistically significant Spatial Autocorrelation phenomenon in the

    model residuals, which is evidence that you are missing one or more key explanatory variables. In regression analysis, problems with Spatial Autocorrelation residuals often have the phenomenon of clustering: high predictors cluster together and low predictors cluster together. Spatial Autocorrelation analysis can be performed on the residual field, if the P & lt; 0.05, indicating that your model is missing key explanatory variables.

  6. Model Performance Evaluation After the above five conditions are

    met, the superiority and inferiority of the model can be evaluated by correcting the R2 value. R2 values range from 0 to 1 and are expressed as a percentage. Suppose you are modeling the crash rate and find a model that passes all five of the previous checks with a corrected R2 value of 0.7. So you can see that the explanatory variable in the model says that the crash rate is 70%, or that the model explains 70% of the change in the dependent variable of the crash rate. Different fields require different values of R2 . In some scientific fields, 25% of the explanation of complex phenomena is enough to be exciting, while in some fields, the value of R2 may need to be close to 80% to be satisfactory.

    The AICc value is also often used to judge the model, and the smaller the AICc value is, the more suitable it is for the observed data.

Related topics

Regression analysis

Geographically Weighted Regression Analysis

Basic vocabulary

Measuring Geographic Distributions

Clustering Distribution

Analysis Mode