There are various types of map projections, generally classified by two criteria: classification by distortion characteristics and classification by construction methods.
Classification by Distortion Characteristics
Based on distortion characteristics, projections can be categorized as: Conformal projection, Equal-area projection, and Arbitrary projection.
- Conformal Projection
Preserves shape similarity of infinitesimal elements. The scale factor remains constant at any given point (indicatrix circle), though radii vary between points. At large scales, projected shapes may not fully match actual ground features. Ideal for navigation charts and wind/current maps requiring accurate angular measurements. Not suitable for area measurement due to significant area distortion.
- Equal-area Projection
Maintains relative area proportions, suitable for thematic maps requiring precise area comparisons such as geological, soil, land use, and administrative maps.
- Arbitrary Projection
Neither conformal nor equal-area, these projections balance all distortions moderately. A special subtype called Equidistant projection preserves true distances along specific lines (meridians in normal aspect or vertical circles in oblique/transverse aspects). Commonly used in educational maps, scientific reference maps, and general world maps.
Classification by Construction Methods
Projections can be divided into two groups based on construction methods: Geometric projections and Analytical projections.
Geometric projections transfer the graticule onto developable geometric surfaces (plane, cone, cylinder), then flatten the surface. Includes Azimuthal, Conic, and Cylindrical projections. Subclassified by surface orientation: Normal, Transverse, and Oblique aspects. See illustration:
 |
Azimuthal Projection: Uses a planar surface tangent/secant to the ellipsoid. Distortion increases radially from the point/line of contact.
Conic Projection: Employs a conical surface tangent/secant to the ellipsoid. Particularly suitable for mid-latitude regions elongated along parallels. Widely used in Chinese national mapping.
Cylindrical Projection: Utilizes a cylindrical surface tangent/secant to the ellipsoid. Typically used for equatorial regions and world maps.
Analytical projections derive graticules through mathematical formulae without geometric surfaces, including: Pseudoazimuthal, Pseudoconic, Pseudocylindrical, and Polyconic projections.
Pseudoazimuthal Projection: Modified azimuthal projection. In normal aspect, parallels remain concentric circles; all meridians except the central one become curves converging at the pole.
Pseudocylindrical Projection: Adapted from cylindrical projection. Parallels stay straight lines; meridians (except central) become symmetrical curves about the central meridian.
Pseudoconic Projection: Derived from conic projection. Parallels remain circular arcs; meridians (except central) curve symmetrically about the central meridian.
Polyconic Projection: Conceptualized using multiple tangent cones. Parallels are non-concentric arcs with centers along the central meridian, which remains straight while other meridians curve symmetrically.
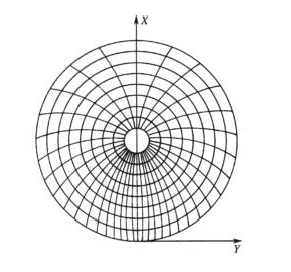 |
 |
| Fig: Schematic of Graticule in Pseudoazimuthal Projection (Source: Internet) | Fig: Schematic of Graticule in Pseudocylindrical Projection (Source: Internet) |
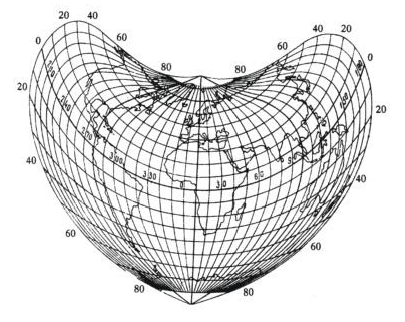 |
 |
| Fig: Schematic of Graticule in Pseudoconic Projection (Source: Internet) | Fig: Schematic of Graticule in Polyconic Projection (Source: Internet) |
- Geometric Projection
- Analytical Projection
Related Topics



