Overlay analysis involves processing or analyzing spatial data to extract new spatial geometry information required by the user. For example, if we need to understand the soil distribution within a certain administrative region, we can perform overlay analysis using the national land use map and the administrative region planning map datasets to obtain the desired results. Additionally, overlay analysis can also process various attributes of the data.
Overlay analysis is widely used in fields such as resource management, urban construction evaluation, land management, agriculture, forestry, animal husbandry, and statistics.
Spatial overlay analysis involves operations such as logical intersection, logical union, logical difference, and XOR. For ease of discussion, Euclidean space layers A, B, and C are defined as binary images here. The table below introduces the properties and laws of Boolean logical operations for layers.
| Logical Operation | Definition | Properties | Description |
| Contain | If for all x∈A, x∈B, then A is called a sub-image of B or B contains A, denoted as A⊆B. | (1) A⊆A
(2) A⊆B,B⊆C ⇒ A⊆C (3) A⊆B,B⊆A ⇒ A=B |
If A⊆B and A≠B, A is called a proper sub-image of B, denoted as A⊂B. We use Ω to denote an image and φ to denote an empty image. |
| Intersection | The intersection of A and B is defined as A∩B = {x|x∈A and x∈B} | (1) A∩A = A
(2) A∩φ = φ (3) (A∩B)∩C = A∩(B∩C) |
If A∩B = φ, A and B are said to be disjoint. |
| Union (OR) | The union (also called OR) of A and B is defined as A∪B = {x|x∈A or x∈B} | (1) A∪A = A
(2) A∪φ = A (3) (A∪B)∪C = A∪(B∪C) |
|
| Difference | The difference of A and B is defined as A-B = {x|x∈A, and x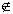 B} B} |
(1)A-φ = A
(2) A-A = φ (3) (A-B)-C = A-(B∪C) |
|
| XOR | The XOR of A and B is defined as: A⊕B = {x|x∈A or x∈B, and x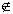 A∩B} A∩B} |
The following figure shows the Boolean logical operations: containment, intersection, union, difference, and XOR.

Instructions for Use
The region datasets participating in overlay analysis must not contain overlapping polygon objects. Datasets with overlapping polygon objects are invalid, and the system cannot guarantee the correctness of the overlay results. It is recommended to perform topology validation before conducting overlay analysis.
Overlapping polygons are illustrated in the figure below:

Notes
- In the two datasets used for overlay analysis, the dataset used for the analysis can be of types such as point, line, or polygon, and is referred to as the input dataset (called the first dataset in SuperMap GIS). The other dataset is a region dataset and is referred to as the overlay dataset (called the second dataset in SuperMap GIS).
- It should be noted that the region dataset or record set itself should avoid containing overlapping areas; otherwise, the overlay analysis results may be incorrect.
- All datasets involved in overlay analysis must share the same geographic reference system, including input data and result data.
- In cases where the data volume for overlay analysis is large, it is necessary to create a spatial index for the result dataset to improve data display speed.
Related Topics
Introduction to Overlay Analysis Tools



