Definition
The Thiessen polygon method, proposed by Dutch climatologist A.H.Thiessen, calculates average rainfall by connecting discrete weather stations into triangles and constructing perpendicular bisectors of triangle edges. These bisectors form polygons around each station, where the rainfall intensity from the single contained station represents the entire polygon area.
Also known as Voronoi diagrams, Thiessen polygons consist of perpendicular bisectors connecting adjacent points. Key characteristics include:
- Each polygon contains exactly one discrete point
- Any location within a polygon is closest to its contained point
- Points on polygon edges are equidistant to two adjacent discrete points
Applications
Used for qualitative analysis, statistics, and proximity analysis, Thiessen polygons partition space into regions allocated to nearest point features. They serve as alternatives to interpolation for generalizing sample measurements, such as:
- Generalizing weather station measurements to surrounding areas
- Creating service area models for retail stores
- Determining adjacent points through polygon edges (n-sided polygon indicates n neighbors)
- Enabling nearest-neighbor identification without distance calculations
Steps
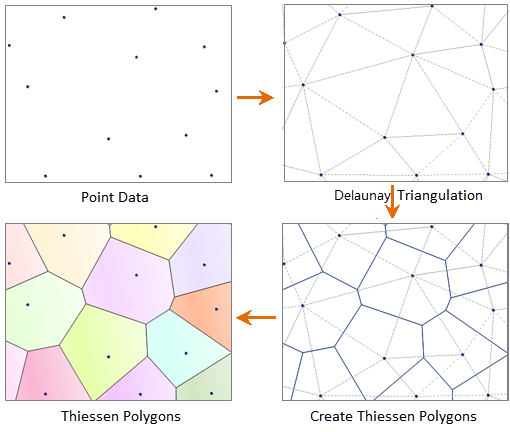
The core algorithm involves Delaunay triangulation. Construction process:
- Scan points left-right and top-down, ignoring points within proximity tolerance
- Build Delaunay triangulation, numbering points and triangles while recording adjacency relationships
- Create polygon edges using triangle edge perpendicular bisectors, with intersections as vertices
- Original points become polygon anchors
 |
| Figure: Steps to Construct Thiessen Polygon |
Related Topics
Thiessen Polygon Application Example



