所有类

概要:
嵌套 |
字段 |
构造器 |
方法

详细资料:
字段 |
构造器 |
方法

java.lang.Object
- com.supermap.data.InternalHandle
- - com.supermap.data.InternalHandleDisposable
  - - com.supermap.analyst.spatialanalyst.InterpolationParameter
    - - com.supermap.analyst.spatialanalyst.InterpolationKrigingParameter

所有已实现的接口:

IDisposable
```
public class InterpolationKrigingParameter
extends InterpolationParameter
```
克吕金（Kriging）内插法参数类，继承自 InterpolationParameter 类。该类为 Kriging 插值算法提供必要的参数信息，包括半变函数类型、自相关阈值、基台值、块金效应值。
Kriging 法为地质统计学上一种空间资料内插处理方法，主要的目的是利用各数据点间变异数（variance）的大小来推求某一未知点与各已知点的权重关系，再由各数据点的值和其与未知点的权重关系推求未知点的值。Kriging 法最大的特色不仅是提供一个最小估计误差的预测值，并且可明确的指出误差值的大小。一般而言，许多地质参数，如地形面本身即具有连续的性质，故在一短距离内的任两点必有空间上的关系。反之，在一不规则面上的两点若相距甚远，则在统计意义上可视为互为独立 (stastically indepedent)，这种随距离而改变的空间上连续性，可用半变异图 (semivariogram) 来表现。因此，若想由已知的散乱点来推求某一未知点的值，则可利用半变异图推求各已知点及欲求值点的空间关系。再由此空间参数推求半变异数，由各数据点间的半变异数可推求未知点与已知点间的权重关系，进而推求出未知点的值。

克吕金法的优点是以空间统计学作为其坚实的理论基础。物理含义明确；不但能估计测定参数的空间变异分布，而且还可以估算参数的方差分布。克吕金法的缺点是计算步骤较烦琐，计算量大，且变异函数有时需要根据经验人为选定。

克吕金插值法可以采用两种方式来获取参与插值的采样点，进而获得相应位置点的预测值，一个是在待计算预测值位置点周围一定范围内，获取该范围内的所有采样点，通过特定的插值计算公式获得该位置点的预测值；另一个是在待计算预测值位置点周围获取一定数目的采样点，通过特定的插值计算公式获得该位置点的预测值。

克吕金插值过程是一个多步骤的处理过程，包括：

1.创建变异图和协方差函数来估计统计相关（也称为空间自相关）的值；

2.预测待计算位置点的未知值。

半变异函数与半变异图：

计算所有采样点中相距 h 个单位的任意两点的半变异函数值，那么任意两点的距离 h 一般是唯一的，将所有的点对的距离与相应的半变函数值快速显示在以 h 为 X 坐标轴和以半变函数值为 Y 坐标轴的坐标空间内，就得到了半变异图。相距距离愈小的点其半变异数愈小，而随着距离的增加，任两点间的空间相依关系愈小，使得半变异函数值趋向于一稳定值。此稳定值我们称之为基台值（Sill）；而达到基台值时的最小 h 值称之为自相关阈值（Range）。

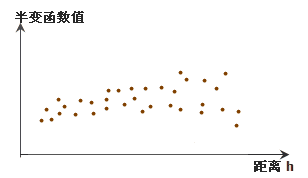
某半变异图

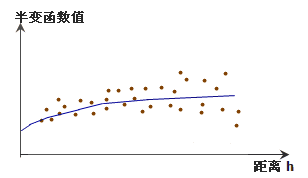
某半变异函数拟合曲线图

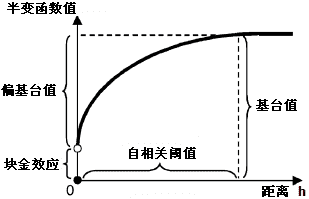
有关概念示意图

块金效应：

当点间距离为 0（比如，步长=0）时，半变函数值为 0。然而，在一个无限小的距离内，半变函数通常显示出块金效应，这是一个大于 0 的值。如果半变函数在Y周上的截距式 2 ，则块金效应值为 2。

块金效应属于测量误差，或者是小于采样步长的小距离上的空间变化，或者两者兼而有之。测量误差主要是由于观测仪器的内在误差引起的。自然现象的空间变异范围很大（可以在很小的尺度上，也可以在很大的尺度上）。小于步长尺度上的变化就表现为块金的一部分。

半变异图的获得是进行空间插值预测的关键步骤之一，克吕金法的主要应用之一就是预测非采样点的属性值，半变异图提供了采样点的空间自相关信息，根据半变异图，选择合适的半变异模型，即拟合半变异图的曲线模型。

不同的模型将会影响所获得的预测结果，如果接近原点处的半变异函数曲线越陡，则较近领域对该预测值的影响就越大。因此输出表面就会越不光滑。

SuperMap 支持的半变函数模型有指数型、球型和高斯型。详细信息参见 VariogramMode 类。

完成模型的确定后，就可以使用选定的模型，对采样点数据进行插值分析了。
示范代码:
以下代码示范了根据给定的点数据集、用于插值的字段和目标数据源进行插值分析，并且选择克吕金插值法进行插值。
```
 public void interpolationKriging(){
                    // 获取用来进行插值分析的点数据集
                    Workspace workspace = new Workspace();
                    DatasourceConnectionInfo datasourceConnectionInfo = new DatasourceConnectionInfo("G:\\Data\\ElevationPoints.udb", "ElevationPoints", "");
                    Datasource targetDatasource = workspace.getDatasources().open(datasourceConnectionInfo);
                    DatasetVector datasetElevPoints = (DatasetVector)targetDatasource.getDatasets().get("elevationpoints");

                    //获得一个合法的名称作为结果数据集的的名称
                    String resultDatasetName = targetDatasource.getDatasets().getAvailableDatasetName("resultDatasetGrid");

                    //设置克吕金内插法参数
                    InterpolationKrigingParameter interpolationMethodKrigingParam = new InterpolationKrigingParameter();
                    interpolationMethodKrigingParam.setExpectedCount (5);
                    interpolationMethodKrigingParam.setBounds(datasetElevPoints.getBounds());
                    interpolationMethodKrigingParam.setResolution ( 285);
                    interpolationMethodKrigingParam.setSearchMode  ( SearchMode.KDTREE_FIXED_COUNT);
                    interpolationMethodKrigingParam.setVariogramMode  ( VariogramMode.EXPONENTIAL);

                    //调用插值分析类的插值分析方法实现对点数据集的插值，并获得分析结果
                    DatasetGrid resultInterpolationGrid = Interpolator.interpolate(interpolationMethodKrigingParam, datasetElevPoints, "ELEV", 0.7, targetDatasource, resultDatasetName, PixelFormat.SINGLE);

                    //释放工作空间占有的资源
                    workspace.dispose();
        }
```

构造器概要

构造器
构造器和说明
`InterpolationKrigingParameter()` 构造一个 InterpolationKrigingParameter 的新对象。
`InterpolationKrigingParameter(double resolution, SearchMode searchMode, double searchRadius, int expectedCount, VariogramMode variogramMode)` 根据指定的参数来构造一个 InterpolationKrigingParameter 的新对象。
`InterpolationKrigingParameter(InterpolationAlgorithmType type)` 根据指定的参数来构造一个 InterpolationKrigingParameter 的新对象。
`InterpolationKrigingParameter(InterpolationAlgorithmType type, double resolution, SearchMode searchMode, double searchRadius, int expectedCount, VariogramMode variogramMode)` 根据指定的参数来构造一个 InterpolationKrigingParameter 的新对象。

方法概要

所有方法实例方法具体方法
限定符和类型	方法和说明
`double`	`getAngle()` 返回克吕金算法中旋转角度值。
`Exponent`	`getExponent()` 返回用于插值的样点数据中趋势面方程的阶数。
`double`	`getMean()` 返回插值字段的平均值，即采样点插值字段值总和除以采样点数目。
`double`	`getNugget()` 返回块金效应值。
`double`	`getRange()` 返回自相关阈值。
`double`	`getSill()` 返回基台值。
`InterpolationAlgorithmType`	`getType()` 返回插值算法类型。
`VariogramMode`	`getVariogramMode()` 返回克吕金（Kriging）插值时的半变函数类型。
`void`	`setAngle(double value)` 设置克吕金算法中旋转角度值。
`void`	`setExponent(Exponent exponent)` 设置用于插值的样点数据中趋势面方程的阶数。
`void`	`setMean(double value)` 设置插值字段的平均值，即采样点插值字段值总和除以采样点数目。
`void`	`setNugget(double value)` 设置块金效应值。
`void`	`setRange(double value)` 设置自相关阈值。
`void`	`setSill(double value)` 设置基台值。
`void`	`setVariogramMode(VariogramMode variogramMode)` 设置克吕金（Kriging）插值时的半变函数类型。
`String`	`toString()` 返回一个表示 InterpolationKrigingParameter 对象的字符串。

从类继承的方法 com.supermap.analyst.spatialanalyst.InterpolationParameter
dispose, getBounds, getExpectedCount, getMaxPointCountForInterpolation, getMaxPointCountInNode, getResolution, getSearchMode, getSearchRadius, setBounds, setExpectedCount, setMaxPointCountForInterpolation, setMaxPointCountInNode, setResolution, setSearchMode, setSearchRadius

从类继承的方法 com.supermap.data.InternalHandleDisposable
makeSureNativeObjectLive

从类继承的方法 java.lang.Object
equals, getClass, hashCode, notify, notifyAll, wait, wait, wait

- 构造器详细资料
  - InterpolationKrigingParameter
```
public InterpolationKrigingParameter()
```
    构造一个 InterpolationKrigingParameter 的新对象。
  - InterpolationKrigingParameter
```
public InterpolationKrigingParameter(InterpolationAlgorithmType type)
```
    根据指定的参数来构造一个 InterpolationKrigingParameter 的新对象。
    
    参数:
    
    type - 指定的插值分析的算法类型。
  - InterpolationKrigingParameter
```
public InterpolationKrigingParameter(double resolution,
                                     SearchMode searchMode,
                                     double searchRadius,
                                     int expectedCount,
                                     VariogramMode variogramMode)
```
    根据指定的参数来构造一个 InterpolationKrigingParameter 的新对象。
    
    参数:
    
    resolution - 指定的插值运算所获得的栅格数据集的分辨率。
    
    searchMode - 指定的插值运算时查找参与运算点的查找方式。
    
    searchRadius - 指定的插值运算时查找参数运算点的查找范围。
    
    expectedCount - 指定的参与插值运算的点数。
    
    variogramMode - 指定的半变函数类型。
  - InterpolationKrigingParameter
```
public InterpolationKrigingParameter(InterpolationAlgorithmType type,
                                     double resolution,
                                     SearchMode searchMode,
                                     double searchRadius,
                                     int expectedCount,
                                     VariogramMode variogramMode)
```
    根据指定的参数来构造一个 InterpolationKrigingParameter 的新对象。
    
    参数:
    
    type - 指定的插值分析算法类型。
    
    resolution - 指定的插值运算所获得的栅格数据集的分辨率。
    
    searchMode - 指定的插值运算时查找参与运算点的查找方式。
    
    searchRadius - 指定的插值运算时查找参数运算点的查找范围。
    
    expectedCount - 指定的参与插值运算的点数。
    
    variogramMode - 指定的半变函数类型。
- 方法详细资料
  - getVariogramMode
```
public VariogramMode getVariogramMode()
```
    返回克吕金（Kriging）插值时的半变函数类型。
    目前支持球型函数、指数函数和高斯函数类型，详情请参见 VariogramMode 类型。
    
    返回:
    
    克吕金插值时的半变函数类型。
    
    另请参阅:
    
    VariogramMode
    
    默认值:
    
    默认值为 VariogramMode.SPHERICAL。
  - setVariogramMode
```
public void setVariogramMode(VariogramMode variogramMode)
```
    设置克吕金（Kriging）插值时的半变函数类型。目前支持球型函数、指数函数和高斯函数类型，详情请参见VariogramMode类型。
    
    参数:
    
    variogramMode - 克吕金插值时的半变函数类型。
    
    另请参阅:
    
    VariogramMode
  - getRange
```
public double getRange()
```
    返回自相关阈值。
    自相关阈值是指当一个半变函数在达到一定距离的时候，曲线的趋势不能够再增长，即趋于水平，那么曲线最初开始水平的距离称为自相关阈值。
    
    返回:
    
    自相关阈值。
    
    默认值:
    
    默认值为 0.0。
  - setRange
```
public void setRange(double value)
```
    设置自相关阈值。
    自相关阈值是指当一个半变函数在达到一定距离的时候，曲线的趋势不能够再增长，即趋于水平，那么曲线最初开始水平的距离称为自相关阈值。
    
    参数:
    
    value - 自相关阈值。
  - getSill
```
public double getSill()
```
    返回基台值。
    基台值是指半变函数达到变长范围时，Y 轴上的值。
    有关概念示意图：
    
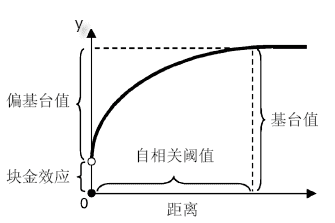
    返回:
    
    基台值。
    
    默认值:
    
    默认值为0。
  - setSill
```
public void setSill(double value)
```
    设置基台值。
    半变异函数值趋向于一稳定值时，此稳定值我们称之为基台值。
    有关概念示意图：
    
    参数:
    
    value - 基台值。
    
    默认值:
    
    默认值为0。
  - getAngle
```
public double getAngle()
```
    返回克吕金算法中旋转角度值。此角度值指示了每个查找邻域相对于水平方向逆时针旋转的角度。
    
    返回:
    
    克吕金插值过程中旋转角度大小。
    
    默认值:
    
    默认值为 0.0。
  - setAngle
```
public void setAngle(double value)
```
    设置克吕金算法中旋转角度值。此角度值指示了每个查找邻域相对于水平方向逆时针旋转的角度。
    
    参数:
    
    value - 旋转角度值。
  - getNugget
```
public double getNugget()
```
    返回块金效应值。
    当点间距离为 0（比如，步长=0）时，半变函数值为 0。然而，在一个无限小的距离内，半变函数通常显示出块金效应，这是一个大于 0 的值。如果半变函数在 Y 轴上的截距是 2 ，则块金为 2。
    块金效应属于测量误差，或者是小于采样步长的小距离上的空间变化，或者两者兼而有之。测量误差主要是由于观测仪器的内在误差引起的。自然现象的空间变异范围很大（可以在很小的尺度上，也可以在很大的尺度上）。小于步长尺度上的变化就表现为块金的一部分。
    有关概念示意图：
    
    返回:
    
    块金效应值。
    
    默认值:
    
    默认值为 0.0。
  - setNugget
```
public void setNugget(double value)
```
    设置块金效应值。
    当点间距离为 0（比如，步长=0）时，半变函数值为 0。然而，在一个无限小的距离内，半变函数通常显示出块金效应，这是一个大于 0 的值。如果半变函数在 Y 轴上的截距是 2 ，则块金为 2。
    块金效应属于测量误差，或者是小于采样步长的小距离上的空间变化，或者两者兼而有之。测量误差主要是由于观测仪器的内在误差引起的。自然现象的空间变异范围很大（可以在很小的尺度上，也可以在很大的尺度上）。小于步长尺度上的变化就表现为块金的一部分。
    有关概念示意图：
    
    参数:
    
    value - 块金效应值。
  - getMean
```
public double getMean()
```
    返回插值字段的平均值，即采样点插值字段值总和除以采样点数目。此属性只适用于简单克吕金方法。
    
    返回:
    
    插值字段的平均值。
    
    默认值:
    
    默认值为 0.0。
  - setMean
```
public void setMean(double value)
```
    设置插值字段的平均值，即采样点插值字段值总和除以采样点数目。此属性只适用于简单克吕金方法。
    
    参数:
    
    value - 插值字段的平均值。
  - getExponent
```
public Exponent getExponent()
```
    返回用于插值的样点数据中趋势面方程的阶数。详情请参见 Exponent 类。此属性只适用于泛克吕金方法。
    
    返回:
    
    趋势面方程的阶数。
    
    默认值:
    
    默认值为 Exponent.EXP1。
  - setExponent
```
public void setExponent(Exponent exponent)
```
    设置用于插值的样点数据中趋势面方程的阶数。详情请参见 Exponent 类。此属性只适用于泛克吕金方法。
    
    参数:
    
    exponent - 指定的用于插值的样点数据中趋势面方程的阶数。
  - getType
```
public InterpolationAlgorithmType getType()
```
    返回插值算法类型。
    
    指定者:
    
    getType 在类中 InterpolationParameter
    
    返回:
    
    插值算法的类型。
    
    另请参阅:
    
    InterpolationAlgorithmType
  - toString
```
public String toString()
```
    返回一个表示 InterpolationKrigingParameter 对象的字符串。
    
    覆盖:
    
    toString 在类中 InterpolationParameter
    
    返回:
    
    一个表示 InterpolationKrigingParameter 对象的字符串。

跳过导航链接

所有类

概要:
嵌套 |
字段 |
构造器 |
方法

详细资料:
字段 |
构造器 |
方法

类 InterpolationKrigingParameter

构造器概要

方法概要

从类继承的方法 com.supermap.analyst.spatialanalyst.InterpolationParameter

从类继承的方法 com.supermap.data.InternalHandleDisposable

从类继承的方法 java.lang.Object

构造器详细资料

InterpolationKrigingParameter

InterpolationKrigingParameter

InterpolationKrigingParameter

InterpolationKrigingParameter

方法详细资料

getVariogramMode

setVariogramMode

getRange

setRange

getSill

setSill

getAngle

setAngle

getNugget

setNugget

getMean

setMean

getExponent

setExponent

getType

toString