Thiesson Polygon Definition
Dutch meteorologist A.H.Thiessen proposed a method of calculating average precipitation based on the precipitation measurements at discretely distributed meteorological stations. In the method, all the neighboring stations are connected to form a series of triangles. Then the perpendicular bisectors of the triangle sides are drawn. For each station, the bisectors surrounding it form a polygon. The precipitation in the polygon region can then be represented by the precipitation measured at that station, which is also the only station within the polygon. This polygon is named Thiessen polygon.
Thiessen polygon is also called Voronoi diagram. Thiessen polygons are polygons whose boundaries define the area that is closest to each point relative to all other points. Features of Thiessen polygons are:
- Every Thiessen polygon contains only one discrete point;
- For any location in a Thiessen polygon, the discrete point associated with that polygon is the closest one among all the discrete points;
- The points located on a side of a Thiessen polygon have equal distance to the two discrete points defining that side.
Thiesson Polygon Application
Thiessen polygons can be used for qualitative analysis, statistical analysis, proximity analysis, etc.. Polygon features created by creating Thiessen polygons can divide the available space and assigned the space to the nearest point feature. Thiessen polygons are sometimes used in place of the interpolation operation to generalize a set of sample measurement values to the area nearest to them. We can generalize a set of measurement values from climate measurement instruments to the surrounding area, and also build service area model for a group of shops quickly. For example:
- The nature of discrete points can be used to describe the nature of Thiessen Polygon area;
- Data of discrete points can be used to calculate data of Thiessen polygon areas;
- While we are analyzing which discrete points are adjacent to a discrete point, we can directly obtain the result according to Thiessen polygons. If Thiessen polygons is n-gon, then there are n adjacent discrete points.
- When a point falls into a Thiessen polygon, it is nearest to the corresponding discrete point, without the need of calculating the distance.
Steps for Thiessen Polygon Construction
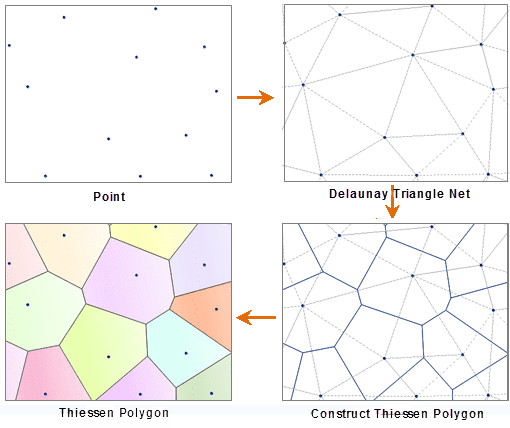
Steps for creating Thiessen polygons are as follows:
- The points used to create the Thiessen Polygons are scanned from left to right and top to bottom. Points closer than the chosen proximal tolerance to previously scanned points are ignored.
- All points are triangulated into a triangulated irregular network (TIN) that meets the Delaunay criterion.
- The perpendicular bisectors for each triangle edge are constructed to form the edges of the Thiessen polygons and their intersections become the polygon vertices.
- Points constructing Thiessen polygons are anchors.