Transformation Models and Scope of Application

SuperMap desktop products support five types of coordinate transformation models: Position Vector (7-para), Coordinate Frame (7-para), China_3D_7P (7-para), China_2D_7P (7-para), and China_2D_4P (4-para).

Transformation Models

Position Vector (7-para), Coordinate Frame (7-para): These two methods are commonly referred to as the seven-parameter transformation or Bursa model, including three translation parameters, three rotation parameters, and one scale factor. They can be considered as one model, with the only difference being the sign convention for rotation defined by different countries.

Position Vector (European definition): Counterclockwise rotation is negative.
Coordinate Frame (U.S. and Australian definition): Counterclockwise rotation is positive.

China_3D_7P (7-para): The three-dimensional seven-parameter transformation model is used for point coordinate transformation between geodetic coordinate systems under different earth ellipsoid datums. It involves three translation parameters, three rotation parameters, and one scale factor, while also accounting for the differences in the semi-major axis and flattening of the two earth ellipsoids corresponding to the two geodetic coordinate systems.
China_2D_7P (7-para): The two-dimensional seven-parameter transformation model is used for point coordinate transformation from a geocentric coordinate system to a geodetic coordinate system under different earth ellipsoid datums. It involves three translation parameters, three rotation parameters, and one scale factor.
China_2D_4P (4-para): The two-dimensional four-parameter transformation model is used for coordinate transformation between different Gaussian projection planes within a local area. It involves two translation parameters, one rotation parameter, and one scale parameter. For three-dimensional coordinates, the coordinates must first be converted to plane coordinates via Gaussian projection before calculating the transformation parameters.

Scope of Application

The selection of a transformation model is influenced by the coordinate system of the control points and the transformation area. Users can refer to the scope of application of transformation models provided in the "Technical Specification for Geodetic Control Point Coordinate Transformation" and choose the appropriate transformation model based on the coordinate system of the source data control points and the applicable area range of the transformation model.

Position Vector (7-para), Coordinate Frame (7-para): Suitable for space rectangular coordinate transformation of control points at the provincial and national levels.
China_3D_7P (7-para): Suitable for coordinate transformation of control points at the provincial and national levels with an ellipsoidal surface of 3° or larger.
China_2D_7P (7-para): Suitable for coordinate transformation of control points at the provincial and national levels with an ellipsoidal surface of 3° or larger.
China_2D_4P (4-para): Suitable for small-scale planar coordinate transformation of control points and establishing the connection between relatively independent planar coordinate systems and the 2000 National Geodetic Coordinate System.

The following table shows the selection of coordinate transformation models and their scope of application for transforming control points from different coordinate systems to the 2000 National Geodetic Coordinate System:

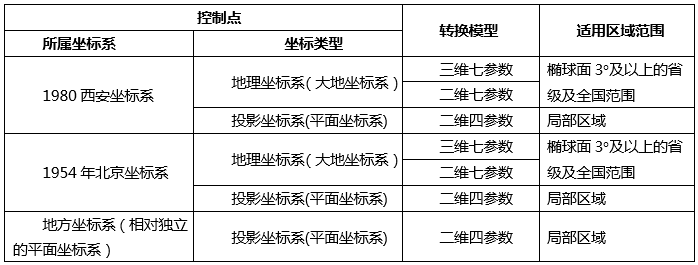Application Scenarios

With SuperMap desktop, users can convert data from a local coordinate system to the 2000 National Geodetic Coordinate System without relying on other plugins, achieving transformation results under different coordinate systems.

If the local coordinate system is derived from a common coordinate system (e.g., Xian 1980, Beijing 1954, etc.), converting the local coordinate system to the 2000 National Geodetic Coordinate System requires first converting the local coordinate system to the actual common coordinate system, and then converting from the common coordinate system to the 2000 National Geodetic Coordinate System. In SuperMap desktop, this can be achieved through the following steps:

Step 1: Convert the local coordinate system to the common coordinate system: Use the "Reproject Dataset" function, select the two-dimensional four-parameter (China_2D_4P) transformation model, and convert the local coordinate system to the actual common coordinate system.

Step 2: Convert the common coordinate system to the 2000 National Geodetic Coordinate System: Use the "Calculate Transformation Model Parameters" function to calculate the transformation parameters, then use the "Reproject Dataset" function, selecting transformation models such as two-dimensional seven-parameter (China_2D_7P), three-dimensional seven-parameter (China_3D_7P), or Coordinate Frame, to achieve the conversion from the common coordinate system to the 2000 National Geodetic Coordinate System.

If the local coordinate system is based on a real coordinate system within a certain projection zone, it can be directly converted to the 2000 National Geodetic Coordinate System using Step 2 above.

Model Expressions

Position Vector (7-para), Coordinate Frame (7-para)

China_3D_7P (7-para)

China_2D_7P (7-para)

China_2D_4P (4-para)

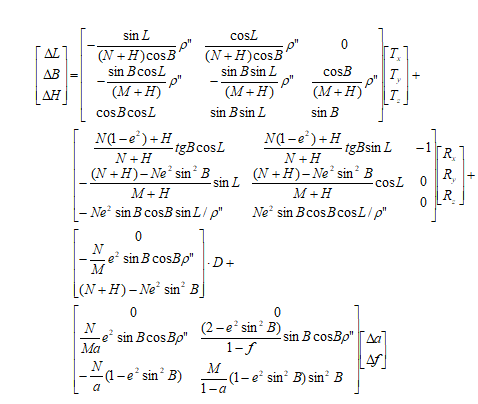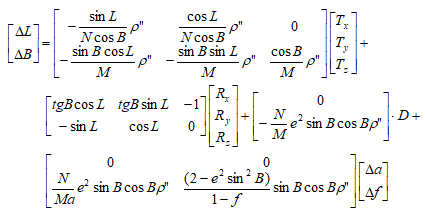Notes:

When user data is in a Gauss-Krüger projected coordinate system, note that the horizontal and vertical coordinate values in this projected coordinate system are opposite to the XY coordinates in the application, meaning the Gauss-Krüger coordinate values are (Y, X), while the application displays them as (X, Y).