The application provides four registration methods: Linear Registration, Quadratic Polynomial Registration, Rectangular Registration, and Offset Registration.
Linear Registration
Linear registration, also known as affine transformation, assumes different actual scales in X and Y directions caused by map deformation, thus enabling map distortion correction. Let x, y represent original coordinates of input image, and X, Y represent corrected output coordinates. The coordinate transformation formula is:
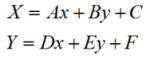 |
There are six parameters (A, B, C, D, E, F) in the formula, which can be determined by selecting corresponding control points between the registration layer and reference layer. Theoretically, at least three non-collinear control point pairs are required to solve these parameters. When setting constant terms C and F to 0, a minimum of four points are needed. In practice, four or more control points are typically used for linear registration. Parameters are solved using least squares method.
Linear transformation is the most commonly used registration method. By considering deformations in both X and Y directions, it produces output coordinates through scaling, rotation, translation, etc., resulting in different length ratios across directions.
Quadratic Polynomial Registration
Quadratic polynomial registration is a high-precision method that treats original image distortion as a curved surface while outputting to a regular plane. Theoretically, any surface can be approximated by sufficiently high-order polynomials. A quadratic polynomial can effectively correct severely distorted images with high accuracy. The correction formula is:
 |
This formula contains 12 parameters. While six control point pairs theoretically suffice for transformation, at least seven pairs are generally required for higher accuracy. Increasing control points significantly improves image registration precision. Polynomial coefficients are derived using least squares method. Compared with linear correction (which is essentially first-order polynomial registration), quadratic polynomial registration requires more control point pairs and corrects more complex distortions.
Rectangular Registration
Rectangular registration is a special constrained linear registration. When both original and corrected images are regular rectangles, selecting two diagonal corner points can determine coordinates for all four corners. By setting constant terms in linear registration formula to 0, two diagonal points suffice to derive correction parameters. This method saves time and avoids error accumulation from multiple control points. However, as output errors are not calculated, it's considered a low-precision rough correction method.
Offset Registration
Offset registration requires only one control-reference point pair. It calculates X and Y coordinate differences, then applies these offsets to all coordinates in the original dataset.
 Note:
Note:Offset registration skips error calculation. It achieves alignment by applying X/Y axis offsets calculated from coordinate differences between source and target points.
Related Topics



