Thiessen Polygon Definition

Thiessen Polygon is a method proposed by Dutch climatologist A. H. Thiessen to calculate the average rainfall based on the rainfall of discrete meteorological stations, that is, all adjacent meteorological stations are connected to form a triangle, and the vertical bisector of each side of the triangle is drawn. A number of perpendicular bisectors around each weather station then form a polygon. The rainfall intensity in the polygon area is represented by the rainfall intensity of a unique weather station contained in the polygon, and the polygon is called Thiessen Polygon.

Thiessen Polygon, also known as Voronoi diagram, is a continuous polygon composed of a set of perpendicular bisectors connecting two adjacent points. Thiessen Polygon is characterized by:

• Each Thiessen Polygon contains only one discrete point of data;
• The point in the Thiessen Polygon is closest to the corresponding discrete point;
• The points on the Thiessen Polygon are equidistant from the discrete points on either side of it.

Thiessen Polygon Applications

Thiessen Polygon can be used for qualitative analysis, Statistic Analysis, Proximity Analysis, etc. Polygon features created by creating Thiessen Polygon divide the available space and assign it to the nearest point feature. Thiessen Polygon is sometimes used as an alternative to interpolation to generalize a set of sample measurements to the area closest to them. Using Thiessen Polygon, measurements taken from a group of climate gauges can be generalized to the surrounding area, and a service area model can be quickly built for a group of stores. For example:

The properties of Thiessen Polygon region
• can be described by the properties of discrete points.
The data of the Thiessen Polygon area
• can be calculated using the data of the discrete points;
When
• a discrete point is adjacent to other discrete points, it can be obtained directly according to Thiessen Polygon, and if Thiessen Polygon is an n-polygon, it is adjacent to n discrete points;
• When a data point falls into a Thiessen Polygon, it is closest to the corresponding discrete point, and there is no need to calculate the distance.

Thiessen Polygon Creation Procedure

establish Thiessen Polygon algorithm is to reasonably connect discrete data points into a triangular network, that is, to construct a Delaunay triangular network. The steps to establish Thiessen Polygon are as follows:

Scan point data of the Thiessen Polygon
1. to be established from left to right and from top to bottom. If the distance between a point and the previous scanning point is less than given adjacent tolerance value, the point will be ignored during the analysis.
Constructing a Delaunay triangulation network by
2. the discrete point data, numbering the discrete points and the constructed triangles, recording which discrete point forms each triangle, and simultaneously recording the numbers of all triangles adjacent to each discrete point;
3. Draw the perpendicular bisectors of the sides of each triangle. These perpendicular bisectors form the sides of the Thiessen Polygon. The intersection of the perpendicular bisectors is the vertex of the corresponding Thiessen Polygon.
The point
4. used to establish the Thiessen Polygon becomes the anchor point of the corresponding Thiessen Polygon.

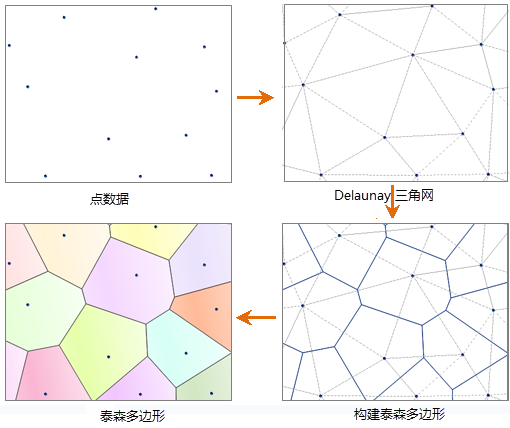Figure: Construct Thiessen Polygon step

Related topics

Construct Thiessen Polygon

Thiessen Polygon Application Example