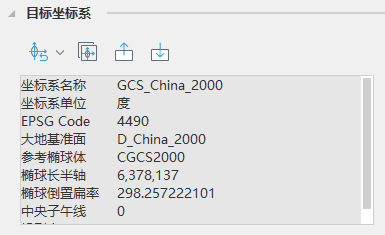
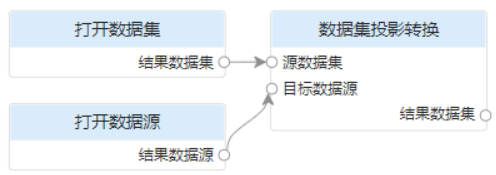
使用说明
根据目标投影坐标系对数据集进行投影转换，转换后的数据集保存在目标数据源中。
根据所设置的“投影转换方法”的不同，该工具的参数设置也会不同。投影转换方法一般可概括分为三参数转换方法、七参数转换方法：
-
三参数转换法
参照系转换时，比较简单的转换方法是所谓的三参数转换法。这种转化方法所依据的数学模型是认为两种大地参照系之间仅仅是空间的坐标原点发生了平移，而不考虑其他因素（见图1）。这种方法必然产生三个参数，X 、Y、Z 三个方向的平移量。三参数转换法计算简单，但精度较低，一般用在不同的地心空间直角坐标系之间的转换。
-
七参数转换法
七参数法依据的数学模型不仅考虑了坐标系的平移，同时还考虑了坐标系旋转、尺度不一等因素。所以需要的参数除了三个平移量外，还要三个旋转参数（又称三个尤拉角）和比例因子（又叫尺度因子）。转换原理如图2所示。三个平移量用ΔX、ΔY、ΔZ 表示，三个旋转转换参数用 Rx，Ry，Rz 表示；比例因子用 S 表示。其中比例因子表示从原坐标系转换到新坐标系的尺度伸缩量。一般情况下，平移因子的单位为米（与坐标系单位保持一致），旋转角度的单位是秒，比例因子的单位为百万分之一。
- 地心转换法(the Geocentric Translation)、莫洛金斯基转换法（Molodensky）、简化的莫洛金斯（MolodenskyAbridged）转换法属于精度较低的投影转换方法。三参数转换法需要三个平移转换参数（ΔX，ΔY，ΔZ），莫洛金斯基转换法、简化的莫洛金斯基转换法也要三个平移转换参数（ΔX，ΔY，ΔZ）。在数据精度要求不高的情况下一般可以采用这几种方法。
- 位置矢量法（Position Vector）、基于地心的七参数转换法（Coordinate Frame）、布尔莎方法（Bursa-Wolf）属于精度较高的几种转换方法。需要七个参数来进行调整和转换，包括三个平移转换参数（ΔX，ΔY，ΔZ）、三个旋转转换参数（Rx，Ry，Rz）和一个比例参数（S）。这几种方法是完全相同的，只是由于国家地区或测量学派的不同，习惯称谓不同。
在实际的工作中，采用哪种转换方法要视具体情况而定。转换结果满意与否取决于转换参数的设置情况。转换参数的获取可以从官方测量机构、数据提供商处得到；也可以自行实测，推算转换参数。转换参数合适与否，必须通过两个参照系中都存在的控制点确定。
参数说明
| 参数名 | 默认值 | 参数释义 | 参数类型 |
|---|---|---|---|
| 源数据集 | 待进行投影转换的源数据集。在iServer的处理自动化WebUI界面中，可以通过点击参数右侧的“设置”按钮，在“设置连接信息”对话框中完成数据集的指定，并且支持多种数据源类型中数据集。
另外，还可通过“打开数据集”工具，打开一个数据集，然后，将返回的数据集通过连接的方式赋值给“数据集投影转换”工具的“源数据集”输入参数，如下图所示，这样，模型执行时，打开的数据集就动态赋值给“数据集投影转换”工具的对应参数。 
由此可见，“数据集坐标系转换”工具的“源数据”输入参数也是可以通过连接，从其他处理自动化工具输出的结果数据集传入。 |
Dataset | |
| 目标坐标系 | 源数据转换后的目标坐标系。在iServer的处理自动化WebUI界面中，该参数需要输入坐标系对应的EPSG编码，例如：该参数值为：4326，表示WGS 1984地理坐标系；而在iDesktopX处理自动化界面中，该参数可以通过对话框来设置，如下图所示：
。 |
PrjCoordSys | |
| 目标数据源 | 指定的存储投影转换后的结果数据集的数据源。在iServer的处理自动化WebUI界面中，可以通过点击参数右侧的“设置”按钮，在“设置连接信息”对话框中完成数据源的指定，并且支持多种数据源类型。 另外，还可通过“打开数据源”工具，打开一个数据源，然后，将返回的数据源通过连接的方式赋值给“数据集投影转换”工具的“目标数据源”输入参数，如下图所示，这样，模型执行时，打开的数据源就动态赋值给“目标数据源”参数。 
|
Datasource | |
| 结果数据集名 | 指定投影转换后的结果数据集的名称。 | String | |
| 比例差 | 0.0 | 该参数为比例因子，表示从原坐标系转换到新坐标系的尺度伸缩量。 | Double |
| 旋转角度 X | 0.0 | 旋转转换参数，表示 X 轴的旋转角度，单位是：秒。 | Double |
| 旋转角度 Y | 0.0 | 旋转转换参数，表示 Y 轴的旋转角度，单位是：秒。 | Double |
| 旋转角度 Z | 0.0 | 旋转转换参数，表示 Z 轴的旋转角度，单位是：秒。 | Double |
| 偏移量 X | 0.0 | X 轴的坐标偏移量（偏移量也称为平移量）。 | Double |
| 偏移量 Y | 0.0 | Y 轴的坐标偏移量（偏移量也称为平移量）。 | Double |
| 偏移量 Z | 0.0 | Z 轴的坐标偏移量（偏移量也称为平移量）。 | Double |
| 旋转原点 X 坐标 | 0.0 | 旋转原点的 X 坐标的量。 | Double |
| 旋转原点 Y 坐标 | 0.0 | 旋转原点的 Y 坐标的量。 | Double |
| 旋转原点 Z 坐标 | 0.0 | 旋转原点的 Z 坐标的量。 | Double |
| 投影转换方法 | MTHGEOCENTRICTRANSLATION | 投影转换所使用的方法。SuperMap提供了几种常用的投影转化方法，具体参见下面的“投影转换方法”表格。 | CoordSysTransMethod |
表格：投影转换方法
| 名称 | 描述 |
|---|---|
| MTHGEOCENTRICTRANSLATION | GeocentricTranslation 基于地心的三参数转换法。 |
| MTH MOLODENSKY | 莫洛金斯基(Molodensky)转换法，三参数转换法。 |
| MTH MOLODENSKY ABRIDGED | MolodenskyAbridged 简化的莫洛金斯基转换法，三参数转换法。 |
| MTH POSITION VECTOR | PositionVector 位置矢量法，七参数转换法。 |
| MTH COORDINATE_FRAME | CoordinateFrame 基于地心的七参数转换法，七参数转换法。 |
| MTH BURSA WOLF | Bursa-Wolf方法，七参数转换法。 |
| MolodenskyBadekas | 莫洛金斯基-巴待卡斯投影转换方法，一种十参数的空间坐标转换模型。 |
| China3D7P | 三维七参数转换模型，用于不同坐标系与2000国家大地坐标系(CGC2000)之间的转换。适用于全国及省级椭球面3度及以上不同地球椭球基准下的大地坐标系统间控制点坐标转换。模型涉及三个平移参数，三个旋转参数和一个尺度变化参数，同时需要顾及两种大地坐标系所对应的两个地球椭球体长半轴和扁率差。 |
| China2D7P | China2D7P二维七参数转换模型，用于不同坐标系与2000国家大地坐标系（CGC2000）之间的转换。适用于全国及省级适用于椭球面3度及以上不同地球椭球基准下的大地坐标系统间控制点坐标转换。模型涉及三个平移参数，三个旋转参数和一个尺度变化参数。对于1954年北京坐标系、1980西安坐标系向2000国家大地坐标系的转换，由于两个参心系下的大地高的精度较低，建议采用二维七参数转换。 |
| China2D4P | 二维四参数转换模型，用于不同坐标系与2000国家大地坐标系（CGC2000）之间的转换。适用于省级及以下局部2度以内局部范围控制点坐标转换。模型涉及三个平移参数和一个尺度变化参数。 |
| MTH_Prj4 | PROJ4 Transmethod投影转换算法，该算法基于PROJ4 第三方投影转换工具，从而支持更多的投影转换操作，满足更多海外用户的数据投影转换需求，该投影转换算法只支持有对应EPSG Code的投影之间的转换。 |
| MTH_EXTENTION | 用户通过SuperMap提供投影扩展功能，通过编写自定义的转换算法，实现投影以及地理坐标系的转换。 |
| BD09toGCJ02 | 百度坐标系转火星坐标系。 |
| GCJ02TOBD09 | 火星坐标系转百度坐标系。 |
| GCJ02TOWGS84 | 火星坐标系转WGS84。 |
| WGS84TOGCJ02 | WGS84转火星坐标系。 |
输出结果
| 参数名 | 参数释义 | 参数类型 |
|---|---|---|
| 结果数据集 | 结果数据集 | Dataset |