The direction distribution can reflect the spatial characteristics of the distribution center, discrete trend and diffusion direction of the features. The method is calculated by using the mean center as the starting point to calculate the standard deviation of the x coordinates and the y coordinates, thus defining the axis of the ellipse, so the ellipse is called the standard deviation ellipse.
Applications
- Mapping the distributional trend for a set of crimes might identify a relationship to particular physical features (a string of bars or restaurants, a particular boulevard, and so on).
- Mapping groundwater well samples for a particular contaminant might indicate how the toxin is spreading and, consequently, may be useful in deploying mitigation strategies.
- Comparing the size, shape, and overlap of ellipses for various racial or ethnic groups may provide insights regarding racial or ethnic segregation.
- Plotting ellipses for a disease outbreak over time may be used to model its spread.
Function Entrances
- Spatial Analysis > Spatial Statistical Analysis > Measuring Geographic Distributions > Directional Distribution. (iDesktop)
- Spatial Statistical Analysis > Measuring Geographic Distributions > Directional Distribution. (iDesktopX)
- Toolbox > Spatial Statistical Analysis > Measuring Geographic Distributions > Directional Distribution. (iDesktopX)
Main Parameters
- Source Dataset :Set up the vector data sets to be analyzed, supports points, lines, and regions three types of datasets.
-
Ellipse Size : Set up the level of the result ellipse, according to the data contained in the results, the range of data is divided into three levels, different standard deviation levels, and the resulting center points will be different.
- One Standard Deviation: the result range of the first level standard deviation can be included in the source data center of about 68%.
- Two Standard Deviations: the result range of the second standard deviation can be included in the data center of about 95%.
- Three Standard Deviations: the result range of the third standard deviation can be included in the data center of about 98%.
- Group Field :Refers to a field that divides the analysis elements into categories. After classification, each group of objects has a central element. The Group Field can be of integer, date, or string type. Records with NULL values for the Group Field will be excluded from the analysis.
- Weight Field :Set up a numeric field for weight, for example: rank as weight field with a traffic accident, the results ellipse can not only reflect the spatial distribution of the accident can also reflect the severity of the traffic accident.
- Keep Statistics Field :Refers to the retention field that sets the result data in the field list box, and the statistical type of the field value.
- Result Settings :Set up the datasource for the result data and the dataset name.
Results Description
The output is a region dataset and has the following attribute fields. The application renders the field “flat” of the result dataset and the grouping field of the source dataset on the map.
| Field Names | Attribute Significance |
|---|---|
| CircleCenterX | The x-coordinate of the center of the circle |
| CircleCenterX | The y-coordinate of the center of the circle |
| SemiMajorAxis | semi-major axis |
| SemiMinorAxis | semi-minor axis |
| RotationAngle | Elliptical direction (The angle between the semimajor axis and the north direction) |
| district_Group | grouping field |
| flat | ellipse oblateness |
- The semi-major axis reflects the direction of the greater dispersion degree, and the semi-minor axis reflects the high degree of concentration.
- The larger the difference between the semi-major axis and the semi-minor axis (the larger the oblateness), the more obvious the direction of the data. Conversely, the closer the difference between the semi-major axis and semi-minor axis, the less obvious the directivity of the data.
- If the length of semi-major axis and the semi-minor axis are exactly the same, that’s a circle. The circle indicates that there is no directional characteristic.
Instance
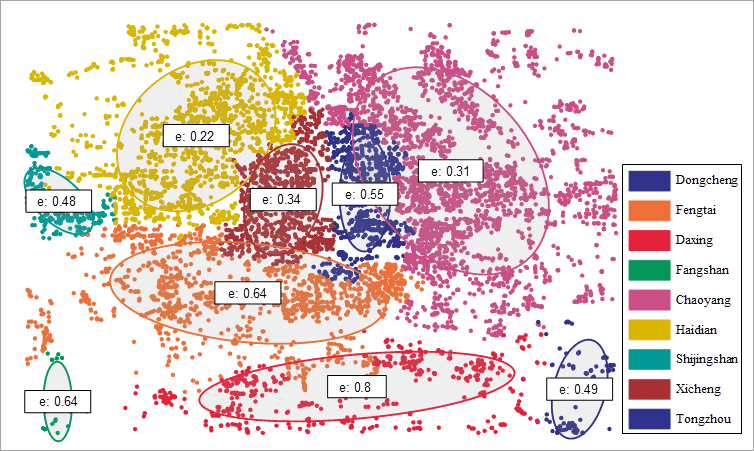
The analysis of the medical center can obtain the distribution trend. As the following picture shows, the standard deviation ellipse oblateness (0.8) of Daxing is the largest, indicating that the distribution of medical points in this area has the most obvious directionality.