Path analysis is one of the commonly used network analysis functions. In real life, we often need to find the shortest path between two points, which holds significant importance for transportation, firefighting, information transmission, and emergency rescue operations. During transportation, we aim to identify routes with minimal costs; during disaster response, we prioritize paths that take the least time.

Traveling Salesman Problem (TSP) analysis is an unordered path analysis. The salesman can decide the order of visiting nodes, with the goal of achieving the smallest (or near-smallest) total travel impedance. Its key difference from optimal path analysis lies in the handling of node visitation order when traversing all network nodes. Optimal path analysis must follow a specified node sequence, while TSP analysis allows flexible determination of visitation order.

As shown below, this illustrates the results of performing optimal path analysis and TSP analysis using the same set of stops.

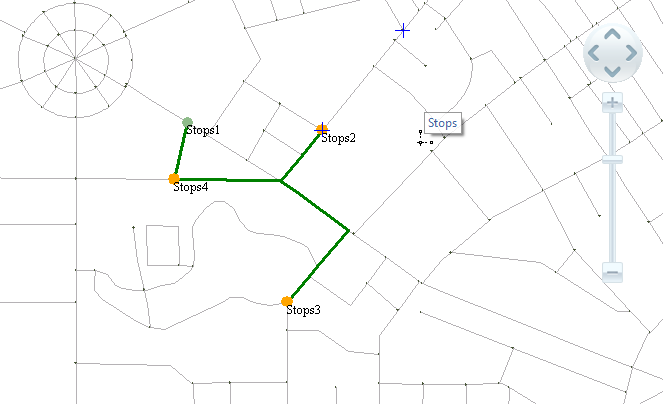
SuperMap GIS's TSP analysis requires specifying a start node, with the first node being the default origin. If an end node is specified, the salesman must visit it last. When the start node and end node are identical (i.e., the salesman must return to the origin), simply set this point as both the origin and destination.

In TSP analysis, nodes are categorized into four types: origin, destination, intermediate points, and origin-destination point. Depending on node configurations, results may fall into the following scenarios:

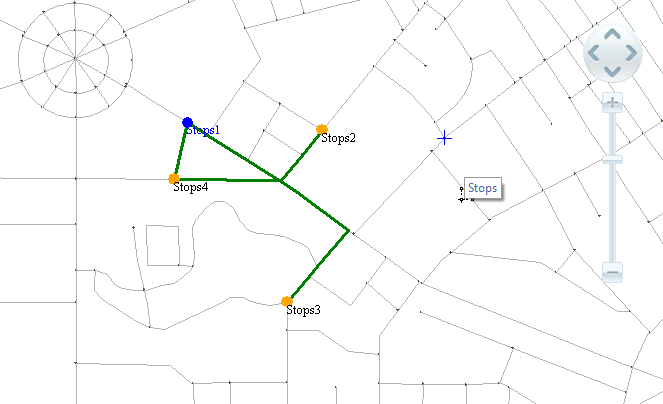
• Specifying only an origin: The application iteratively determines the optimal travel route from the origin based on minimal cost principles. As shown in Figure 2, when Stop 1 is set as the origin, the analysis result will start from Stop 1 and sequentially pass through other intermediate points following minimal route cost.
• Specifying both origin and destination: The application calculates the optimal route from the origin to the destination, with intermediate analysis iteratively determining the best path using minimal cost principles. As shown in Figure 3, when Stop 1 (Chaoyang Park) is set as the origin and Stop 5 (South Lake Park) as the destination, the analysis result will start at Stop 1 and ultimately reach Stop 5.
• Specifying an origin-destination point: This refers to setting the same location as both origin and destination. The analysis calculates the optimal route starting and ending at this point while maintaining minimal travel cost. As shown in Figure 4, when Stop 1 (Chaoyang Park) is set as the origin-destination point, the analysis result will start from Stop 1 and return to the same location.