Linear Referencing

Linear referencing is a method that uses relative descriptions along linear features with measurement values to describe and store geographic locations. Distance measurements (which can represent attributes like length, time, or cost) are used to locate events along linear features. As a common dynamic positioning technique, linear referencing is widely applied in data capture for linear features (e.g., roads, railways, rivers), public transit management, pavement quality management, and simulations of utility networks (power grids, telephone lines, TV cables, water pipelines).

Two main reasons explain the preference for linear referencing in real-world applications:

1. People naturally use distance-based descriptions along linear features for positioning, which is more intuitive than traditional (X,Y) coordinates. For example, describing an accident as "300 meters east of XX intersection" is more practical than stating coordinates like (6570.3876,3589.6082).
2. Linear referencing allows associating multiple attribute tables with linear features without splitting lines when attributes change.

As shown below, the gray line represents a highway with mileage measurements. The points and line segment above illustrate two types of events: two traffic accidents occurred at 12 km and 84.3 km markers, while road collapses due to heavy rain affected the section from 35 km to 76 km.

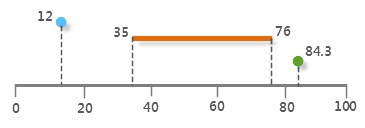Figure: Linear Referencing Schematic

Dynamic Segmentation

Dynamic segmentation does not physically split linear features where attribute changes occur. Instead, based on traditional GIS data models, it stores attributes and corresponding linear features in independent event attribute tables (event tables). During analysis, display, query, or output, linear features are dynamically segmented using distance values from event tables to calculate attribute spatial locations.

In essence, dynamic segmentation visually represents linear referencing features on maps without altering the original spatial data structure, establishing relationships between arbitrary segments and multiple attributes.

Key Concepts

SuperMap's dynamic segmentation primarily involves two data structures: routes and event tables. Routes represent linear features with measurement values, while event tables record locations and attributes of phenomena occurring along routes.

• LineM

  A route is a linear feature with a unique identifier (ID) and measurement system, such as roads, rivers, or pipelines. Each node on a route has an M-value indicating its distance from the starting point.

• M-value

  The M-value represents the distance from a point on the route to its starting point. It operates independently of the dataset's coordinate system and does not require unit consistency.

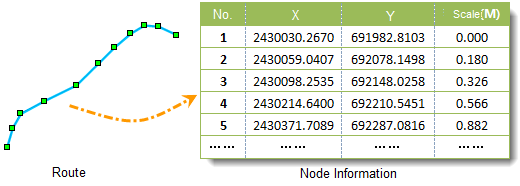
• Route Location

  A route location describes either a point or line segment on a route. Point locations use the route's ID and an M-value, while line segments use the route's ID with start/end M-values.

• Route Dataset

  A dataset storing linear data where each node contains both coordinate values and M-values. Route datasets can be generated by combining linear features with point data.

• Event

  Events are point or line features stored as attribute tables in routing systems, recording route IDs, M-values, and related attributes. Events are categorized into point events and line events.

• Point Event

  Represents precise locations on routes, e.g., mileage markers on highways or accident sites on railways.

• Line Event

  Represents segments along routes, e.g., road maintenance sections.

• Zero-length Event

  A line event where start and end M-values are identical.

• Event Table

  A table storing event conditions, attributes, and routing information, categorized into point event tables and line event tables.

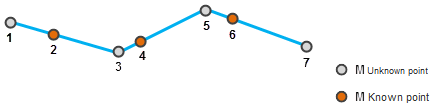
• M-value Interpolation

  Estimates M-values for unknown nodes using interpolation methods: interpolation (between known values) and extrapolation (beyond known ranges). As shown below, node 1's M-value is forward-extrapolated from points 2 and 4; nodes 3 and 5 are interpolated using points 2, 4, 6; node 7 is backward-extrapolated from points 4 and 6.