Raster resampling is the process of assigning pixel values or derived values from the input image to each pixel in the output image. The images mentioned here refer to raster data, including two types: grid (GRID) and image (IMAGE). Resampling is required when the spatial position (after geometric transformation or projection settings) or pixel size (i.e., raster image resolution) changes between input and output images.
Furthermore, raster resampling is a common data processing method for resolving resolution matching issues in spatial analysis. To facilitate analysis, different resolutions are typically converted to the same resolution through resampling. For existing raster data with specific spatial resolution, resampling can create larger pixels (reducing spatial resolution) which may lose detailed information from the original high-resolution data, or create smaller pixels without gaining additional information. Resampling low-resolution multispectral remote sensing imagery to match high-resolution panchromatic imagery enables data fusion that combines high spectral resolution with high spatial resolution, commonly used for thematic extraction and applications in remote sensing.
Raster resampling primarily includes three methods: Nearest Neighbor, Bilinear Interpolation, and Cubic Convolution. The Nearest Neighbor method fills new images with the closest pixel value from the original image, while Bilinear and Cubic Convolution use distance-weighted averages of surrounding pixels. The following sections detail these resampling methods.
Nearest Neighbor
The Nearest Neighbor method assigns the value of the closest pixel in the input raster dataset to the corresponding pixel in the output raster dataset.
This method preserves original raster values and processes quickly, but may cause half-pixel displacement. Suitable for discrete data representing classifications or themes, such as land use or vegetation types.
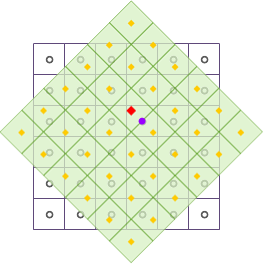 |
As shown in the diagram, after geometric transformations like translation and rotation, the output raster dataset is resampled using the Nearest Neighbor method. Black wireframes represent the input raster dataset, light green fill indicates the output raster dataset, and the red square marks the center position of an output pixel to be updated. The purple dot shows the nearest input pixel center, whose value is assigned to the red square position.
Bilinear Interpolation
The Bilinear Interpolation method calculates new pixel values through weighted averaging of four neighboring pixels (4-neighborhood) in the input raster dataset. Weights are determined by the distance between each neighboring pixel's center and the interpolation point.
This method produces smoother results than Nearest Neighbor but alters original values. Suitable for continuous data representing distributions or surfaces, such as DEM, temperature/precipitation distributions, or slope gradients - data typically derived from interpolated sample points.
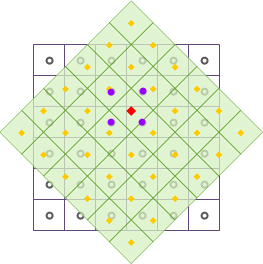 |
As illustrated, after geometric transformations, the output raster dataset is resampled using Bilinear Interpolation. The red square marks an output pixel center to be updated. Four neighboring input pixels (purple dots) are weighted by distance to compute the new value for the red square position.
Cubic Convolution
Similar to Bilinear, Cubic Convolution uses a quintic polynomial interpolation with 16 neighboring pixels (16-neighborhood). Weights depend on distances between these pixel centers and the interpolation point.
This method improves interpolation accuracy through more neighbors, producing sharper results with edge-enhancement effects. However, it's computationally intensive and may produce values outside the original data range. Suitable for aerial photos and remote sensing imagery resampling.
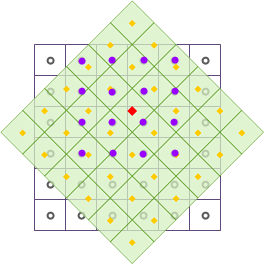 |
The diagram shows Cubic Convolution resampling after geometric transformations. The red square indicates an output pixel center to be updated. Sixteen neighboring input pixels (purple dots) are weighted by distance to calculate the new value for the red square position.
 Related Topics
Related Topics




