Instructions for Use

The dataset is projected and transformed according to the target projected coordinate system, and the transformed dataset is saved in the target data source.

Depending on the "Projection transformation method" set, the parameter settings of this tool will also be different. Projective transformation methods can generally be divided into three-parameter transformation methods and seven-parameter transformation methods:

1. Three-parameter transformation method

   When the frame of reference is converted, the relatively simple conversion method is the so-called three-parameter conversion method. The mathematical model on which this conversion method is based is that only the coordinate origin of the space has shifted between the two geodetic reference systems, without considering other factors (see Figure 1). This method must produce three parameters, the translation in the X, Y, and Z directions. The three-parameter conversion method is simple to calculate, but the accuracy is low, and it is generally used for conversion between different geocentric space Cartesian coordinate systems.

2. Seven parameter conversion method

   The mathematical model based on the seven-parameter method not only considers the translation of the coordinate system, but also considers the rotation of the coordinate system and the different scales. Therefore, in addition to the three translations, the required parameters also need three rotation parameters (also known as the three Euler angles) and a scale factor (also called the scale factor). The conversion principle is shown in Figure 2. The three translations are represented by ΔX, ΔY, and ΔZ; the three rotation transformation parameters are represented by Rx, Ry, Rz; the scale factor is represented by S. Among them, the scale factor represents the scale expansion and contraction from the original coordinate system to the new coordinate system. In general, the unit of the translation factor is meter (consistent with the coordinate system unit), the unit of the rotation angle is second, and the unit of the scale factor is one millionth.

3. The Geocentric Translation, Molodensky, and simplified MolodenskyAbridged transformations are low-precision projection transformation methods. The three-parameter transformation method requires three translation transformation parameters (ΔX, ΔY, ΔZ), and the Molokinsky transformation method and the simplified Molokinsky transformation method also need three translation transformation parameters (ΔX, ΔY, ΔZ). These methods can generally be used when the data accuracy is not high.

4. The position vector method (Position Vector), the geocentric-based seven-parameter conversion method (Coordinate Frame), and the Bursa-Wolf method (Bursa-Wolf) are several conversion methods with high precision. Seven parameters are required for scaling and transformation, including three translational transformation parameters (ΔX, ΔY, ΔZ), three rotational transformation parameters (Rx, Ry, Rz), and one scale parameter (S). These methods are exactly the same, but due to differences in countries, regions or schools of measurement, customary appellations are different.

In actual work, which conversion method to use depends on the specific situation. Whether the conversion result is satisfactory or not depends on the settings of the conversion parameters. Conversion parameters can be obtained from official measurement agencies and data providers; you can also measure and calculate conversion parameters by yourself. The appropriateness of the transformation parameters must be determined by the control points present in both frames of reference.

Parameter Description

parameter name	default value	parameter definition	parameter type
Source dataset		The source dataset to be projected. In iServer's processing automation WebUI interface, you can click the "Settings" button on the right side of the parameter to complete the specification of the data set in the "Set Connection Information" dialog box, and support data sets in multiple data source types. In addition, you can also open a data set through the "Open Data Set" tool, and then connect the returned data set Assign values to the "Source Dataset" input parameters of the "Dataset Projection Transformation" tool, as shown in the figure below, so that when the model is executed, the opened dataset is dynamically assigned to the corresponding parameters of the "Dataset Projection Transformation" tool. 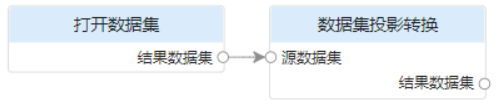It can be seen that the "source data" input parameter of the "dataset coordinate system transformation" tool can also be automated from other processes through connections The resulting dataset output by the tool is passed in.	Dataset
Target coordinate system		The target coordinate system after the source data transformation. In the processing automation WebUI interface of iServer, this parameter needs to input the EPSG code corresponding to the coordinate system, for example: the parameter value is: 4326, indicating the WGS 1984 geographic coordinate system; while in the iDesktopX processing automation interface, this parameter can be entered through the dialog box to set, as shown below: .	PrjCoordSys
Target Data Source		Specifies the data source that stores the result dataset after projection transformation. In the processing automation WebUI interface of iServer, you can click the "Settings" button on the right side of the parameter to complete the data source specification in the "Set Connection Information" dialog box, and support multiple data source types. In addition, you can also use the "Open Data Source" tool to open a data source, and then assign the returned data source to the "Target Data Source" input parameter of the "Dataset Projection Transformation" tool through connection, as follows As shown in the figure, in this way, when the model is executed, the opened data source is dynamically assigned to the "target data source" parameter.	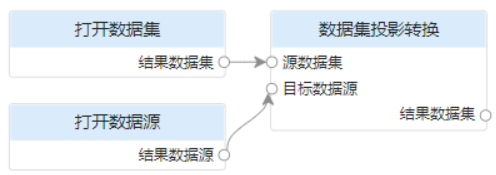Datasource
Result dataset name		Specify the name of the result dataset after projection transformation.	String
Scale difference	0.0	This parameter is a scale factor, which means the scale expansion from the original coordinate system to the new coordinate system.	Double
rotation angle X	0.0	rotation conversion parameter, indicating the rotation angle of the X axis, the unit is: second.	Double
rotation angle Y	0.0	rotation transformation parameter, which means the rotation angle of the Y axis, and the unit is second.	Double
rotation angle Z	0.0	rotation conversion parameter, indicating the rotation angle of the Z axis, and the unit is second.	Double
Offset X	0.0	Coordinate offset for the X axis (offset is also called translation).	Double
Offset Y	0.0	Coordinate offset of the Y axis (offset is also called translation).	Double
Offset Z	0.0	Coordinate offset of the Z axis (offset is also called translation).	Double
Rotate Origin X Coordinate	0.0	Amount to rotate the X coordinate of the origin.	Double
Rotate Origin Y Coordinate	0.0	Amount to rotate the Y coordinate of the origin.	Double
Rotate Origin Z Coordinate	0.0	Amount to rotate the Z coordinate of the origin.	Double
Projective Transformation Method	MTH_GEOCENTRIC_TRANSLATION	The method to use for the projective transformation. SuperMap provides several commonly used projection transformation methods, see the following "Projection transformation methods" table for details.	CoordSysTransMethod

Table: Projective Transformation Methods |Name|Description |:----|:---- |MTH_GEOCENTRIC_TRANSLATION|GeocentricTranslation Geocentric-based three-parameter translation. | |MTH MOLODENSKY|Molodensky transformation method, three-parameter transformation method. | |MTH MOLODENSKY ABRIDGED|MolodenskyAbridged Simplified Molodensky transformation method, three-parameter transformation method. | |MTH POSITION VECTOR|PositionVector Position vector method, seven parameter conversion method. | |MTH COORDINATE_FRAME|CoordinateFrame The seven-parameter conversion method based on the center of the earth, the seven-parameter conversion method. | |MTH BURSA WOLF|Bursa-Wolf method, seven parameter transformation method. | |MolodenskyBadekas|Molodensky-Badekas projection transformation method, a ten-parameter spatial coordinate transformation model. | |China_3D_7P|The three-dimensional seven-parameter transformation model is used for the transformation between different coordinate systems and the 2000 national geodetic coordinate system (CGC2000). It is suitable for coordinate conversion of control points between geodetic coordinate systems under different earth ellipsoid datums on national and provincial ellipsoid surfaces of 3 degrees and above. The model involves three translation parameters, three rotation parameters and one scale change parameter, and it needs to take into account the semi-major axes and oblateness difference of the two earth ellipsoids corresponding to the two geodetic coordinate systems. |China_2D_7P|China_2D_7P Two-dimensional seven-parameter transformation model, used for transformation between different coordinate systems and the 2000 national geodetic coordinate system (CGC2000). Applicable to the national and provincial levels Applicable to coordinate conversion of control points between geodetic coordinate systems under different earth ellipsoid datums with an ellipsoid of 3 degrees and above. The model involves three translation parameters, three rotation parameters and one scale change parameter. For the conversion from the 1954 Beijing coordinate system and the 1980 Xi’an coordinate system to the 2000 national geodetic coordinate system, due to the low accuracy of the geodetic height under the two ginseng systems, it is recommended to use two-dimensional seven-parameter conversion. |China_2D_4P|The two-dimensional four-parameter transformation model is used for the transformation between different coordinate systems and the 2000 national geodetic coordinate system (CGC2000). It is suitable for coordinate conversion of control points within 2 degrees at the provincial level and below. The model involves three translation parameters and one scale change parameter. |MTH_Prj4|PROJ4 Transmethod projection conversion algorithm, which is based on PROJ4 third-party projection conversion tool, so as to support more projection conversion operations and meet the data projection conversion needs of more overseas users. This projection conversion algorithm only supports the corresponding EPSG Code Conversion between projections. | |MTH_EXTENTION|Users provide projection extension functions through SuperMap, and realize projection and geographic coordinate system conversion by writing custom conversion algorithms. | |BD09toGCJ02|Baidu coordinate system to Mars coordinate system. | |GCJ02TOBD09|Mars coordinate system to Baidu coordinate system. | |GCJ02TOWGS84|Mars coordinate system to WGS84. | |WGS84TOGCJ02|WGS84 to Mars coordinate system. |

output result