Overview

Path analysis is one of the commonly used Network Analysis functions. In real life, we often need to find out the Shortest Path between two points. The solution of this problem is of great significance to traffic, fire protection, information transmission and disaster relief. In the process of transportation, we need to find the path with the least transportation cost; in the process of rescue and disaster relief, we need to find the path with the shortest time.

Traveling Salesman Problem (TSP) Analysis

Traveling Salesman Problem (TSP) Analysis is an unordered path analysis. The traveling salesman can decide the order of visiting the nodes by himself, and the goal is to minimize (or nearly minimize) the sum of the impedances of the travel routes. It differs from Optimal Path Analysis in the way it handles the order in which nodes are accessed in the process of traversing all the nodes in the network. The Optimal Path Analysis must access the nodes in a specified order, while the Traveling Salesman Problem (TSP) Analysis can access the nodes in its own order.

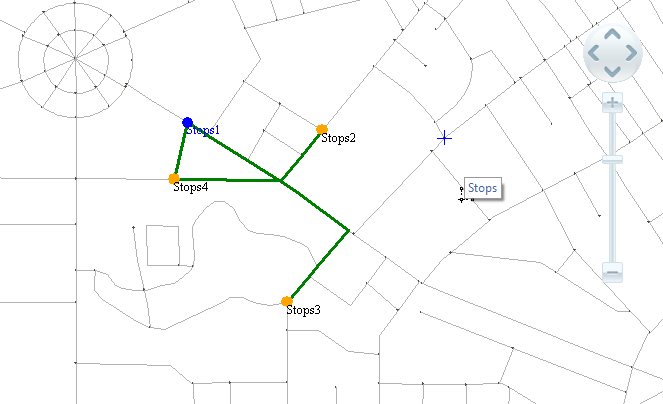
As shown in the figure below, the results of Optimal Path Analysis and Traveling Salesman Problem (TSP) Analysis were performed separately at the same site.

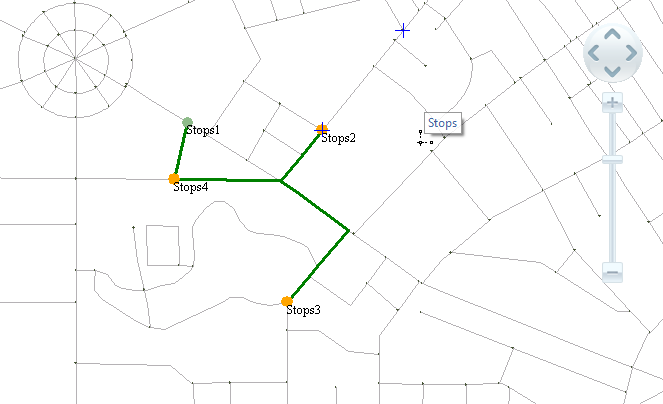
For SuperMap GIS Traveling Salesman Problem (TSP) Analysis, the start node must be specified, and the first node is the starting point by default. If End Node is selected, the traveling salesman must visit End Node last; if the start node and End Node are the same point, that is, the traveling salesman must return to the start node at the end of the trip, this point can be set as the start and end point.

In Traveling Salesman Problem (TSP) Analysis, nodes are divided into four categories: start point, end point, intermediate point, and start and end point. According to different node settings, the results can be divided into the following cases:

• Specify only the starting point: The Application starts from the starting point and iterates to get the best route to travel according to the principle of minimum cost. As shown in Figure 2, designate Site 1 as the starting point. The Analyst Result will start at station 1 and proceed through the other intermediate points in order to minimize the cost of the route.
• Specify the starting point and the end point: Application starts from the starting point to the end point, and the intermediate analysis iterates to get the best route of travel according to the principle of minimum cost. As shown in Figure 3, Station 1 (Chaoyang Park) is designated as the starting point, and Station 5 (South Lake Park) is designated as the end point. The Analyst Result starts at Site 1 and eventually returns to Site 5.
• Specify the start and end points: The start and end points are the same point. The analysis of specified starting and ending points is that the system starts from the starting point to its ending point, and the intermediate analysis iterates to get the best route of travel according to the principle of minimum cost. As shown in Figure 4, Station 1 (Chaoyang Park) is designated as the starting and ending point. Analyst Result starts from Station 1 and finally returns to the location of Station 1.